题目内容
11.已知函数f(x)=a+(bx-1)ex,(a,b∈R)(1)如曲线y=f(x)在点(0,f(0))处的切线方程为y=x,求a,b的值;
(2)若a<1,b=2,关于x的不等式f(x)<ax的整数解有且只有一个,求a的取值范围.
分析 (1)由曲线y=f(x)在(0,f(0))处的切线方程为y=x,得$\left\{\begin{array}{l}{f(0)=0}\\{f′(0)=1}\end{array}\right.$,求出a,b的值即可;
(2)构造函数,通过对构造的函数求导并分类讨论,即可得出a的范围.
解答 解:(1)函数f(x)的定义域是R,f′(x)=bex+(bx-1)ex=(bx+b-1)ex,
∵曲线y=f(x)在点(0,f(0))处的切线方程为y=x,
∴$\left\{\begin{array}{l}{f(0)=0}\\{f′(0)=1}\end{array}\right.$,∴$\left\{\begin{array}{l}{a-1=0}\\{b-1=1}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=1}\\{b=2}\end{array}\right.$;
(2)当b=2时,f(x)=a+(2x-1)ex,(a<1),
关于x的不等式f(x)<ax的整数解有且只有一个,
等价于关于x的不等式a+(2x-1)ex-ax<0的整数解有且只有1个,
构造函数F(x)=a+(2x-1)ex-ax,x∈R,
故F′(x)=ex(2x+1)-a,
1°x≥0时,∵ex≥1,2x+1≥1,故ex(2x+1)≥1,
又a<1,故F′(x)>0,故F(x)在(0,+∞)递增,
∵F(0)=-1+a<0,F(1)=e>0,
∴在[0,+∞)存在唯一整数x0,使得F(x0)<0,即f(x0)<ax0;
2°当x<0时,为满足题意,函数F(x)在(-∞,0)上不存在整数使得F(x)<0,
即F(x)在(-∞,-1]上不存在整数使得F(x)<0,
∵x≤-1,∴ex(2x+1)<0,
①当0≤a<1时,函数F′(x)<0,∴F(x)在(-∞,-1]递减,
∴$\frac{3}{2e}$≤a<1;
②当a<0时,F(--1)=-$\frac{3}{e}$+2a<0,不合题意,
综上,a的范围是[$\frac{3}{2e}$,1).
点评 本题考查导数的几何意义,导数的研究函数中的应用以及不等式问题,意在考查转化和化归思想,数形结合思想以及学生的运算能力.

| 温度x/℃ | 20 | 22 | 24 | 26 | 28 | 30 | 32 |
| 产卵数y/个 | 6 | 10 | 21 | 24 | 64 | 113 | 322 |
| t=x2 | 400 | 484 | 576 | 676 | 784 | 900 | 1024 |
| Z=lny | 1.79 | 2.30 | 3.04 | 3.18 | 4.16 | 4.73 | 5.77 |
| $\overline{x}$ | $\overline{t}$ | $\overline{y}$ | $\overline{z}$ |
| 26 | 692 | 80 | 3.57 |
| $\frac{\sum_{i=1}^{7}({x}_{i}-\overline{x})({y}_{i}-\overline{y)}}{\sum_{i=1}^{7}({x}_{i}-\overline{x})^{2}}$ | $\frac{\sum_{i=1}^{7}({t}_{i}-\overline{t})({y}_{i}-\overline{y})}{\sum_{i=1}^{7}({t}_{i}-\overline{t})^{2}}$ | $\frac{\sum_{i=1}^{7}({z}_{i}-\overline{z})({x}_{i}-\overline{x})}{\sum_{i=1}^{7}({x}_{i}-\overline{x})^{2}}$ | $\frac{\sum_{i=1}^{7}({z}_{i}-\overline{z})({t}_{i}-\overline{t})}{\sum_{i=1}^{7}({t}_{i}-\overline{t})^{2}}$ |
| 1157.54 | 0.43 | 0.32 | 0.00012 |
附:对于一组数据(u1,v1),(u2,v2),…,(un,vn),其回归直线v=βu+α的斜率和截距的最小二乘估计分别为:β=$\frac{\sum_{i=1}^{n}({u}_{i}-\overline{u})({v}_{i}-\overline{v})}{\sum_{i=1}^{n}({u}_{i}-\overline{u})^{2}}$,α=$\overline{v}$-β$\overline{u}$.
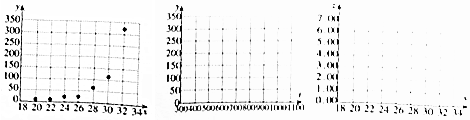
(1)分别画出y关于t的散点图、z关于x的散点图,根据散点图判断哪一个模型更适宜作为回归方程类型?(给出判断即可,不必说明理由).
(2)根据表中数据,分别建立两个模型下建立y关于x的回归方程;并在两个模型下分别估计温度为30℃时的产卵数.(C1,C2,C3,C4与估计值均精确到小数点后两位)(参考数据:e4.65≈104.58,e4.85≈127.74,e5.05≈156.02)
(3)若模型①、②的相关指数计算分别为R12=0.82,R22=0.96,请根据相关指数判断哪个模型的拟合效果更好.
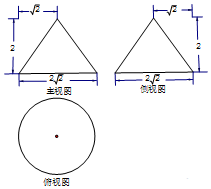 某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的棱长为( )
某工件的三视图如图所示,现将该工件通过切割,加工成一个体积尽可能大的正方体新工件,并使新工件的一个面落在原工件的一个面内,则新工件的棱长为( )| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | $2-\sqrt{2}$ |

| A. | 1991 | B. | 2000 | C. | 2007 | D. | 2008 |
| A. | {1,2} | B. | {1,2,3} | C. | {x|1≤x≤2} | D. | {x|0≤x≤3} |