题目内容

16．执行如图的程序框图，已知输出的s∈[0，4]．若输入的t∈[0，m]，则实数m的最大值为（　　）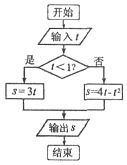
A．1B．2C．3D．4

分析 根据流程图所示的顺序知：该程序的作用是计算一个分段函数的函数值，由条件t的取值范围得分段函数的分类标准，由分支结构中是否两条分支上对应的语句行，易得函数的解析式，从而得解．

解答 解：由s=4t-t2=-（t-2）2+4，
对称轴是t=2，t∈[0，m]，s∈[0，4]，
故s=4t-t2在[0，2）递增，在（2，m]递减，
故s（t）max=s（2）=4，s（t）min=s（0）=s（4）=0，
故m的最大值是4，
故选：D．

点评 本题考查了程序框图的应用问题，解题时应分析程序中各变量、各语句的作用，是基础题目．

练习册系列答案
相关题目
6．某高中有学生2000人，其中高一年级有760人，若从全校学生中随机抽出1人，抽到的学生是高二学生的概率为0.37，现采用分层抽（按年级分层）在全校抽取20人，则应在高三年级中抽取的人数为5．
7．对函数f（x），如果存在x0≠0使得f（x0）=-f（-x0），则称（x0，f（x0））与（-x0，f（-x0））为函数图象的一组奇对称点．若f（x）=ex-a（e为自然数的底数）存在奇对称点，则实数a的取值范围是（　　）
A．（-∞，1）B．（1，+∞）C．（e，+∞）D．[1，+∞）
4．已知椭圆$C：\frac{x^2}{a^2}+\frac{y^2}{2}=1（a＞\sqrt{2}）$的离心率为$\frac{{\sqrt{2}}}{2}$，点M，N是椭圆C上的点，且直线OM与ON的斜率之积为-$\frac{1}{2}$
（Ⅰ）求椭圆C的方程；
（Ⅱ）设动点P（x0，y0）满足$\overrightarrow{OP}$=$\overrightarrow{OM}$+2$\overrightarrow{ON}$，是否存在常数λ，使得P是椭圆$\frac{x^2}{a^2}+\frac{y^2}{2}=λ$上的点．
11．已知函数f（x）=a+（bx-1）ex，（a，b∈R）
（1）如曲线y=f（x）在点（0，f（0））处的切线方程为y=x，求a，b的值；
（2）若a＜1，b=2，关于x的不等式f（x）＜ax的整数解有且只有一个，求a的取值范围．
1．已知$\overrightarrow a=（{1，-1}），\overrightarrow b=（{t，1}）$，若$（{\overrightarrow a+\overrightarrow b}）∥（{\overrightarrow a-\overrightarrow b}）$，则实数t=-1．
8．已知复数z满足（3+2i）z=13i，则z所对应的点位于复平面的第一象限．
5．地铁三号线开通后，某地铁站人流量增大，小A瞄准商机在地铁口投资72万元购得某商铺使用权，且商铺最高使用年限为40年，现小A将该商铺出租，第一年租金为5.4万元，以后每年租金比上一年增加0.4万元，设商铺租出的时间为x（0＜x≤40）年．
（1）求商铺租出x年后的租金总和y；
（2）若只考虑租金所得收益，则出租多长时间能收回成本；
（3）小A考虑在商铺出租x年后，将商铺的使用权转让，若商铺转让的价格F与出租的时间x满足关系式：F（x）=-0.3x2+10.56x+57.6，则何时转让商铺，能使小A投资此商铺所得年平均收益P（x）最大？
6．已知函数f（x）=$\frac{|x|}{x+2}$，若关于x的方程f（x）=kx2有4个不同的实数解，则k的取值范围是（　　）
A．k≥1B．k＞1C．0＜k＜1D．0＜k≤1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网