题目内容
2．（1）在等差数列{an}中，S10=50，S20=300，求通项an．（2）已知正数等比数列{an}的前n项和Sn，且S3=a2+10a1，a5=81，求Sn．
分析 （1）利用等差数列的通项公式与求和公式即可得出．
（2）利用等比数列的通项公式与求和公式即可得出．
解答 解：（1）设公差为d，因为S10=50，S20=300
所以2a1+9d=10 ①…（1分）
2a1+19d=30 ②…（2分）
由①②得 a1=-4 d=2 …（4分）
所以an=2n-6 …（5分）
（2）因为等比数列{an}的各项均为正数，故设公比为q＞0 …（1分）
又S3=a2+10a1，a5=81
所以a1+a2+a3=a2+10a1，${a_1}{q^4}=81$…（2分）
即${a_1}{q^2}=9{a_1}$，${a_1}{q^4}=81$…（3分）
所以${S_n}=\frac{1}{2}（{3^n}-1）$…（5分）
点评 本题考查了等差数列与等比数列的通项公式与求和公式，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目
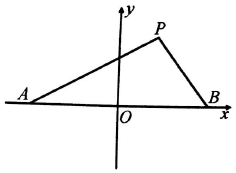如图，设点A，B的坐标分别为（-$\sqrt{3}$，0），（$\sqrt{3}$，0），直线AP，BP相交于点P，且它们的斜率之积为-$\frac{2}{3}$．
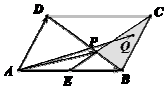如图，在平行四边形ABCD中，点E为边AB的中点，BD与CE交于点P，若$\overrightarrow{AP}=x\overrightarrow{AB}+y\overrightarrow{AD}（x，y∈R）$，则2x+y=；若点Q是△BCP内部（包括边界）一动点，且$\overrightarrow{AQ}=m\overrightarrow{AB}+n\overrightarrow{AD}（m，n∈R）$，则m+2n的取值范围为[1，3]．
11．已知正实数x，y满足xy=1，若81x2+y2≥m恒成立，则实数m的取值范围为（ ）
| A． | （-∞，9] | B． | （-∞，18] | C． | [9，+∞） | D． | [18，+∞） |
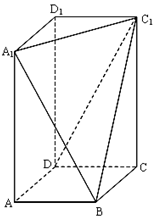已知长方体ABCD-A1B1C1D1，其中AB=BC=2，过A1、C1、B三点的平面截去长方体的一个角后．得到如图所示的，且这个几何体的体积为$\frac{40}{3}$．