题目内容
14．已知集合A={x|x＞-1，x∈R}，集合B={x|x＜2，x∈R}，则A∩B=（-1，2）．分析 根据交集的运算性质计算即可．
解答 解：A={x|x＞-1，x∈R}，B={x|x＜2，x∈R}，
则A∩B=（-1，2），
故答案为：（-1，2）．
点评 本题考查了集合的交集的运算，熟练掌握交集的定义是解题的关键，本题是一道基础题．
练习册系列答案
相关题目
5．把函数f（x）=2sin（x+2φ）（|φ|＜$\frac{π}{2}$）的图象向左平移$\frac{π}{2}$个单位长度之后，所得图象关于直线$x=\frac{π}{4}$对称，且f（0）＜f（$\frac{π}{2}$-φ），则φ=（ ）
| A． | $\frac{π}{8}$ | B． | $\frac{3π}{8}$ | C． | $-\frac{π}{8}$ | D． | $-\frac{3π}{8}$ |
2．已知函数f（x）=|log2|1-x||，若函数g（x）=f2（x）+af（x）+2b有6个不同的零点，则这6个零点之和为（ ）
| A． | 7 | B． | 6 | C． | $\frac{11}{2}$ | D． | $\frac{9}{2}$ |
6．
如图，A1，A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$长轴的左、右端点，O为坐标原点，S，Q，T为椭圆上不同于A1，A2的三点，直线QA1，QA2，OS，OT围成一个平行四边形OPQR，则|OS|2+|OT|2=（ ）
如图，A1，A2为椭圆$\frac{x^2}{9}+\frac{y^2}{5}=1$长轴的左、右端点，O为坐标原点，S，Q，T为椭圆上不同于A1，A2的三点，直线QA1，QA2，OS，OT围成一个平行四边形OPQR，则|OS|2+|OT|2=（ ）| A． | 14 | B． | 12 | C． | 9 | D． | 7 |
3．正方形ABCD与等边三角形BCE有公共边BC，若∠ABE=120°，则BE与平面ABCD所成角的大小为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{2}$ |
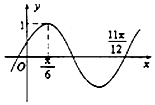已知函数f（x）=sinωx（ω＞0），若函数y=f（x+a）（a＞0）的部分图象如图所示，则ω=2，a的最小值是$\frac{π}{12}$．