题目内容
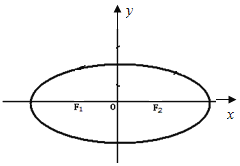
【题目】如图,F1(﹣2,0),F2(2,0)是椭圆C:![]() 的两个焦点,M是椭圆C上的一点,当MF1⊥F1F2时,有|MF2|=3|MF1|.
的两个焦点,M是椭圆C上的一点,当MF1⊥F1F2时,有|MF2|=3|MF1|.
(1)求椭圆C的标准方程;
(2)过点P(0,3)作直线l与轨迹C交于不同两点A,B,使△OAB的面积为![]() (其中O为坐标原点),问同样的直线l共有几条?并说明理由.
(其中O为坐标原点),问同样的直线l共有几条?并说明理由.
【答案】(1)![]() (2)直线l有四条,详见解析
(2)直线l有四条,详见解析
【解析】
(1)根据题意得到![]() 和
和![]() ,联立解得答案。
,联立解得答案。
(2)设直线l的方程为![]() ,利用韦达定理得到
,利用韦达定理得到![]() ,
,
![]() ,利用面积等于
,利用面积等于![]() 得到
得到![]() ,计算得到答案。
,计算得到答案。
(1)由题可知,c=2即a2﹣b2=2﹣﹣﹣﹣①
又∵|MF2|=3|MF1|且|MF1|+|MF2|=2a,∴![]() .
.
又∵MF1⊥F1F2,∴![]() ,即a2=2b2﹣﹣﹣﹣②
,即a2=2b2﹣﹣﹣﹣②
由①②可知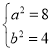 ,∴椭圆C的标准方程为
,∴椭圆C的标准方程为![]() .
.
(2)由题可设直线l的方程为:y=kx+3(k≠0),
令y=0,则x![]() ,即直线l与x轴的交点D坐标为(
,即直线l与x轴的交点D坐标为(![]() ),
),
设点A(x1,y1),点B(x2,y2).
联立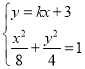 ,消去x,整理可得,(2k2+1)y2﹣6y+9﹣8k2=0,
,消去x,整理可得,(2k2+1)y2﹣6y+9﹣8k2=0,
则有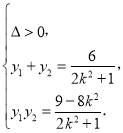
又∵S△AOB=S△ODA+S△ODB
![]() ,
,
∵![]() ,即
,即![]() ,整理可得,k4﹣5k2+4=0,解出k=±1或k=±2.
,整理可得,k4﹣5k2+4=0,解出k=±1或k=±2.
∴直线l有四条.

练习册系列答案
相关题目
【题目】为落实国家扶贫攻坚政策,某社区应上级扶贫办的要求,对本社区所有扶贫户每年年底进行收入统计,下表是该社区扶贫户中![]() 户从2016年至2019年的收入统计数据:(其中
户从2016年至2019年的收入统计数据:(其中![]() 为
为![]() 贫困户的人均年纯收人)
贫困户的人均年纯收人)
年份 | 2016年 | 2017年 | 2018年 | 2019年 |
年份代码 |
|
|
|
|
人均纯收入 |
|
|
|
|
(1)作出贫困![]() 户的人均年纯收人的散点图;
户的人均年纯收人的散点图;
(2)根据上表数据,用最小二乘法求出![]() 关于年份代码
关于年份代码![]() 的线性回归方程
的线性回归方程![]() ,并估计
,并估计![]() 贫困户在2020年能否脱贫(注:国家规定2020年的脱贫标准:人均年纯收入不低于
贫困户在2020年能否脱贫(注:国家规定2020年的脱贫标准:人均年纯收入不低于![]() 元)
元)
(参考公式: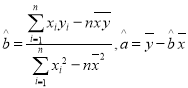 )
)