题目内容
17.已知f(x)=x2-2kx-3k2.(1)若关于x的不等式f(x)<0的解集为∅,求k的取值范围;
(2)解关于x的不等式f(x)<0.
分析 (1)根据不等式f(x)<0的解集为∅,得出△≤0,求出k的取值范围;
(2)关于x的不等式f(x)<0化为x2-2kx-3k2<0,讨论k的取值,求出对应不等式的解集.
解答 解:(1)∵f(x)=x2-2kx-3k2,且不等式f(x)<0的解集为∅,
即x2-2kx-3k2<0的解集为∅,
∴△=4k2+12k2≤0,
解得k=0,
∴k的取值范围是k=0;
(2)关于x的不等式f(x)<0可化为x2-2kx-3k2<0,
且△=4k2+12k2=16k2≥0;
∴当k=0时,不等式的解集为∅;
当k≠0时,不等式对应方程的两个实数根为-3k和5k,
若k>0,则-3k<5k,∴不等式的解集为{x|-3k<x<5k},
若k<0,则5k<-3k,∴不等式的解集为{x|5k<x<-3k};
综上,k=0时,不等式的解集为∅;
k>0时,不等式的解集为{x|-3k<x<5k},
k<0时,不等式的解集为{x|5k<x<-3k}.
点评 本题考查了一元二次不等式与对应方程的应用问题,也考查了含有字母系数的不等式的解法问题,是基础题目.

练习册系列答案
相关题目
9.已知全集U={1,2,3,4,5,6,7},M={1,3,5,7},N={2,5,6,7},则M∪(∁UN)=( )
| A. | {1,3,5,7} | B. | {1,2,4} | C. | {1,3,4,5,7} | D. | {1,3,4,5,6} |
 如图,抛物线开口向下,与x轴交于原点O与点A,顶点为P,△OPA是一个面积为1的等腰直角三角形.
如图,抛物线开口向下,与x轴交于原点O与点A,顶点为P,△OPA是一个面积为1的等腰直角三角形.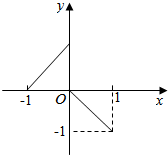 已知函数f(x)的图象如图所示.
已知函数f(x)的图象如图所示.