题目内容
15.用五个数字0、1、1、2、2组成的五位数总共有( )| A. | 24个 | B. | 30个 | C. | 36个 | D. | 48个 |
分析 由题意知先安排特殊元素0,不能排万位,有C41种排法,1与2共有4个元素在四个位置全排列共有A44种排法,其中包含重复的情况,排除11与22的重复排列,得到结果.
解答 解:先安排特殊元素0,不能排万位,有C41种排法,1与2共有A44种排法,排除11与22的重复排列,
共得五位数有$\frac{{C}_{4}^{1}{A}_{4}^{4}}{{A}_{2}^{2}{A}_{2}^{2}}$=24种,
故选:A.
点评 本题考查排列组合的实际应用,是一个数字问题,条件中包含元素0,这是一个特殊的元素,不能排在首位,还有注意本题还有两对重复元素,注意区分.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案
相关题目
5.在数列{an}中,已知a1+a2+…+an=3n-1(n∈N*),则a12+a22+…+a102=( )
| A. | (310-1)2 | B. | $\frac{{{9^{10}}-1}}{2}$ | C. | 910-1 | D. | $\frac{{{3^{10}}-1}}{4}$ |
6.如果一个水平放置的图形的斜二测直观图是一个边长为a的正方形,那么原平面四边形的面积等于( )
| A. | $\frac{{\sqrt{2}}}{4}a$2 | B. | $\frac{{\sqrt{2}}}{2}a$2 | C. | $2\sqrt{2}a$2 | D. | $\frac{{2\sqrt{2}}}{3}a$2 |
10.若$A_{2n}^3=9A_n^3$,则n等于( )
| A. | 12 | B. | 13 | C. | 14 | D. | 15 |
20.在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高二年级有男生1000人,女生800人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高二年级抽取了45名学生的测评结果,并作出频数统计表如下:
表一:男生
表二:女生
(1)计算x,y的值;
(2)由表一表二中统计数据完成下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
表一:男生
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
(2)由表一表二中统计数据完成下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.
| 男生 | 女生 | 总计 | |
| 优秀 | 15 | 15 | 30 |
| 非优秀 | |||
| 总计 | 45 |
4.设数列{an}的前n项和为Sn,若Sn=n2+2n(n∈N*),则$\frac{1}{{a}_{1}{a}_{2}}$+$\frac{1}{{a}_{2}{a}_{3}}$+…+$\frac{1}{{a}_{n}{a}_{n+1}}$=( )
| A. | $\frac{1}{3}-\frac{1}{2n+1}$ | B. | $\frac{1}{3}-\frac{1}{2n+3}$ | C. | $\frac{1}{6}-\frac{1}{4n+3}$ | D. | $\frac{1}{6}-\frac{1}{4n+6}$ |
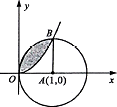 如图所示,阴影部分是由曲线y=x2(x>0)与圆(x-1)2+y2=1构成的区域,在圆中任取一点M,则M点落在阴影部分区域的概率为$\frac{1}{4}$-$\frac{1}{3π}$.
如图所示,阴影部分是由曲线y=x2(x>0)与圆(x-1)2+y2=1构成的区域,在圆中任取一点M,则M点落在阴影部分区域的概率为$\frac{1}{4}$-$\frac{1}{3π}$.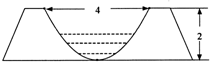 为响应新农村建设,某村计划对现有旧水渠进行改造,已知旧水渠的横断面是一段抛物线弧,顶点为水渠最底端(如图),渠宽为4m,渠深为2m.
为响应新农村建设,某村计划对现有旧水渠进行改造,已知旧水渠的横断面是一段抛物线弧,顶点为水渠最底端(如图),渠宽为4m,渠深为2m.