题目内容
7．将0，1，2，3，4，5这六个数字，每次取三个不同的数字，把其中最大的数字放在百位上排成三位数，这样的三位数有40个．分析 根据百位上的数字可以分为3类，根据分类计数原理可得．
解答 解：第一类，百位为5时，有A52=20个，
第二类，百位为4时，有A42=12个，
第三类，百位为3时，有A32=6个，
第三类，百位为2时，有A22=2个，
根据分类计数原理可得，20+12+6+2=40个，
故答案为：40．
点评 本题考查了分类计数原理，关键是分类，属于基础题．
练习册系列答案
相关题目
18．已知$sin（\frac{π}{6}-α）=cos（\frac{π}{6}+α）$，则tanα=（ ）
| A． | -1 | B． | 0 | C． | $\frac{1}{2}$ | D． | 1 |
16．
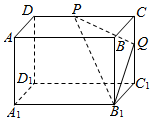在长方体ABCD-A1B1C1D1中，AB=BC=$\sqrt{2}$AA1，P、Q分别是棱CD、CC1上的动点，如图．当BQ+QD1的长度取得最小值时，二面角B1-PQ-D1的余弦值的取值范围为（ ）
在长方体ABCD-A1B1C1D1中，AB=BC=$\sqrt{2}$AA1，P、Q分别是棱CD、CC1上的动点，如图．当BQ+QD1的长度取得最小值时，二面角B1-PQ-D1的余弦值的取值范围为（ ）| A． | [0，$\frac{1}{5}$] | B． | [0，$\frac{\sqrt{10}}{10}$] | C． | [$\frac{1}{5}$，$\frac{\sqrt{10}}{10}$] | D． | [$\frac{\sqrt{10}}{10}$，1] |
17．集合A={x|-2＜x＜1}，B={x|-1＜x＜2}，则A∪B=（ ）
| A． | （-2，1） | B． | （-1，1） | C． | （-2，2） | D． | （-1，2） |