题目内容
函数f（x）=mx+1-m在区间[0，1]上无零点，则m的取值范围是 ．
考点：函数零点的判定定理
专题：计算题,函数的性质及应用
分析：由一次函数及常数函数的单调性可知函数f（x）=mx+1-m在区间[0，1]上无零点可化为f（0）•f（1）＞0，从而求解．
解答：
解：∵函数f（x）=mx+1-m在区间[0，1]上无零点，
∴f（0）•f（1）＞0，
即（1-m）（m+1-m）＞0，
故m＜1；
故答案为：m＜1．
∴f（0）•f（1）＞0，
即（1-m）（m+1-m）＞0，
故m＜1；
故答案为：m＜1．
点评：本题考查了一次函数及常数函数的性质及函数零点的判定定理的应用，属于基础题．
练习册系列答案
相关题目
若二次函数y=x2-2x+1在区间（-∞，a]上为减函数，则a的取值范围是（ ）
| A、a＞1 | B、a≥1 |
| C、a＜1 | D、a≤1 |
如图所示，已知在正方体ABCD-A1B1C1D1中，E是DD1的中点，求证：DB1∥平面A1C1E．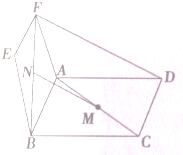
如图，已知?ABCD与?ABEF共边于AB，M，N分别在对角线AC，BF上，且AM：AC=FN：FB．求证：MN∥平面ADF．