题目内容
13.已知复数z=($\frac{1+i}{\sqrt{2}}$)2(其中i为虚数单位),则$\overline{z}$=( )| A. | 1 | B. | -i | C. | -1 | D. | i |
分析 利用复数的运算法则、共轭复数的定义即可得出.
解答 解:z=($\frac{1+i}{\sqrt{2}}$)2=$\frac{2i}{2}$=i,则$\overline{z}$=-i.
故选:B.
点评 本题考查了复数的运算法则、共轭复数的定义,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
4.已知集合A={x|y=lg(x+1)},B={-2,-1,0,1},则(∁RA)∩B=( )
| A. | {-2,-1} | B. | {-2} | C. | {-1,0,1} | D. | {0,1} |
1.在平面直角坐标系xOy中,以(-2,0)为圆心且与直线(3m+1)x+(1-2m)y-5=0(m∈R)相切的所有圆中,面积最大的圆的标准方程是( )
| A. | (x+2)2+y2=16 | B. | (x+2)2+y2=20 | C. | (x+2)2+y2=25 | D. | (x+2)2+y2=36 |
18.已知实数x,y满足$\left\{\begin{array}{l}{x-y+6≥0}\\{x+y≥0}\\{x≤3}\end{array}\right.$若目标函数Z=ax+y的最大值为3a+9,最小值为3a-3,则实数a的取值范围是( )
| A. | {a|-1≤a≤1} | B. | {a|a≤-1} | C. | {a|a≤-1或a≥1} | D. | {a|a≥1} |
5.已知向量$\overrightarrow{OA}=({3,1}),\overrightarrow{OB}=({-1,3})$,$\overrightarrow{OC}=m\overrightarrow{OA}-n\overrightarrow{OB}({m>0,n>0})$,若m+n=1,则$|{\overrightarrow{OC}}$|的最小值为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{10}}}{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
2.已知等比数列{an}满足a1=$\frac{1}{2},{a_2}{a_8}=2{a_5}$+3,则a9=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{9}{8}$ | C. | 648 | D. | 18 |
3.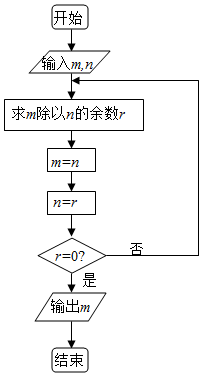 阅读如图所示的程序框图,运行相应的程序,若输入m=168,n=72,则输出m的值为( )
阅读如图所示的程序框图,运行相应的程序,若输入m=168,n=72,则输出m的值为( )
 阅读如图所示的程序框图,运行相应的程序,若输入m=168,n=72,则输出m的值为( )
阅读如图所示的程序框图,运行相应的程序,若输入m=168,n=72,则输出m的值为( )| A. | 72 | B. | 24 | C. | 12 | D. | 6 |
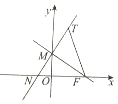 如图,在平面直角坐标中,过F(1,0)的直线FM与y轴交于点M,直线MN与直线FM垂直,且与x轴交于点N,T是点N关于直线FM的对称点.
如图,在平面直角坐标中,过F(1,0)的直线FM与y轴交于点M,直线MN与直线FM垂直,且与x轴交于点N,T是点N关于直线FM的对称点.