题目内容
下列说法正确的是（ ）
| A、函数的极大值大于函数的极小值 |
| B、若f′（x0）=0，则x0为函数f（x）的极值点 |
| C、函数的最值一定是极值 |
| D、在闭区间上的连续函数一定存在最值 |
考点：命题的真假判断与应用
专题：导数的综合应用
分析：A．函数的极大值不一定大于函数的极小值；
B．若f′（x0）=0，则x0为函数f（x）取得极值的必要非充分条件；
C．函数的最值不一定是极值，可能是函数的区间端点的函数值；
D．根据闭区间上连续函数的性质即可得出．
B．若f′（x0）=0，则x0为函数f（x）取得极值的必要非充分条件；
C．函数的最值不一定是极值，可能是函数的区间端点的函数值；
D．根据闭区间上连续函数的性质即可得出．
解答：
解：A．函数的极大值不一定大于函数的极小值，因此不正确；
B．若f′（x0）=0，则x0为函数f（x）取得极值的必要非充分条件，因此不正确；
C．函数的最值不一定是极值，可能是函数的区间端点取得的极值，因此不正确；
D．根据闭区间上连续函数的性质可知：在闭区间上的连续函数一定存在最值，正确．
故选：D．
B．若f′（x0）=0，则x0为函数f（x）取得极值的必要非充分条件，因此不正确；
C．函数的最值不一定是极值，可能是函数的区间端点取得的极值，因此不正确；
D．根据闭区间上连续函数的性质可知：在闭区间上的连续函数一定存在最值，正确．
故选：D．
点评：本题考查了函数极值与最值的关系、闭区间上连续函数的性质，属于基础题．
练习册系列答案
云南师大附小一线名师提优作业系列答案
相关题目
如图，已知椭圆Γ：
按照如图的程序框图执行，若输出结果为31，则M处的条件为（ ）| A、k≥32 | B、k＜16 |
| C、k＜32 | D、k≥16 |
设z=
，若复数z为纯虚数（其中i是虚数单位），则实数a等于（ ）
| 1-ai |
| i |
| A、-1 | ||
| B、0 | ||
| C、1 | ||
D、
|
如图是一个算法框图，则输出的k的值是（ ）
| A、5 | B、6 | C、7 | D、8 |
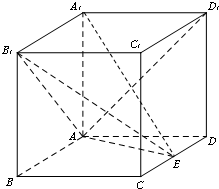在长方体ABCD-A1B1C1D1中，AA1=AD=1，E为线段CD中点．
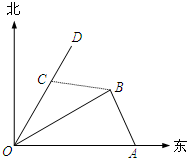如图，港口A在港口O的正东120海里处，小岛B在港口O的北偏东60°的方向，且在港口A北偏西30°的方向上．一艘科学考察船从港口O出发，沿北偏东30°的OD方向以20海里/小时的速度驶离港口O．一艘给养快艇从港口A以60海里/小时的速度驶向小岛B，在B岛转运补给物资后以相同的航速送往科考船．已知两船同时出发，补给装船时间为1小时．