题目内容
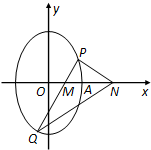
 如图,已知椭圆Γ:
如图,已知椭圆Γ:| x2 |
| b2 |
| y2 |
| a2 |
| ||
| 2 |
(Ⅰ)求椭圆Γ的方程;
(Ⅱ)过点M任作一条直线与椭圆Γ相交于两点P,Q,试问在x轴上是否存在定点N,使得∠PNM=∠QNM,若存在,求出点N的坐标;若不存在,说明理由.
考点:直线与圆锥曲线的综合问题
专题:综合题,圆锥曲线的定义、性质与方程
分析:(Ⅰ)根据离心率e=
,短轴右端点为A,M(1,0)为线段OA的中点,求出几何量,即可求椭圆Γ的方程;
(Ⅱ)分类讨论,设PQ的方程为:y=k(x-1),代入椭圆方程化简,若∠PNM=∠QNM,则kPN+kQN=0,即可得出结论.
| ||
| 2 |
(Ⅱ)分类讨论,设PQ的方程为:y=k(x-1),代入椭圆方程化简,若∠PNM=∠QNM,则kPN+kQN=0,即可得出结论.
解答:
 解:(Ⅰ)由已知,b=2,又e=
解:(Ⅰ)由已知,b=2,又e=
,即
=
,解得a=2
,
所以椭圆方程为
+
=1.…(4分)
(Ⅱ)假设存在点N(x0,0)满足题设条件.
当PQ⊥x轴时,由椭圆的对称性可知恒有∠PNM=∠QNM,即x0∈R; …(6分)
当PQ与x轴不垂直时,设PQ的方程为:y=k(x-1),代入椭圆方程化简得:
(k2+2)x2-2k2x+k2-8=0
设P(x1,y1),Q(x2,y2),则x1+x2=
,x1x2=
则kPN+kQN=
+
=
+
=
=
-
+2x0…(10分)
若∠PNM=∠QNM,则kPN+kQN=0
即k[
-
+2x0]=0,整理得4k(x0-4)=0
因为k∈R,所以x0=4
综上在x轴上存在定点N(4,0),使得∠PNM=∠QNM…(12分)
 解:(Ⅰ)由已知,b=2,又e=
解:(Ⅰ)由已知,b=2,又e=
| ||
| 2 |
| ||
| a |
| ||
| 2 |
| 2 |
所以椭圆方程为
| x2 |
| 4 |
| y2 |
| 8 |
(Ⅱ)假设存在点N(x0,0)满足题设条件.
当PQ⊥x轴时,由椭圆的对称性可知恒有∠PNM=∠QNM,即x0∈R; …(6分)
当PQ与x轴不垂直时,设PQ的方程为:y=k(x-1),代入椭圆方程化简得:
(k2+2)x2-2k2x+k2-8=0
设P(x1,y1),Q(x2,y2),则x1+x2=
| 2k2 |
| 2+k2 |
| k2-8 |
| 2+k2 |
则kPN+kQN=
| y1 |
| x1-x0 |
| y 2 |
| x2-x0 |
| k(x1-1) |
| x1-x0 |
| k(x2-1) |
| x2-x0 |
=
| k(x1-1)(x2-x0)+k(x2-1)(x1-x0) |
| (x 1-x0)(x2-x0) |
| 2(k2-8) |
| 2+k2 |
| 2(1+x0)k2 |
| 2+k2 |
若∠PNM=∠QNM,则kPN+kQN=0
即k[
| 2(k2-8) |
| 2+k2 |
| 2(1+x0)k2 |
| 2+k2 |
因为k∈R,所以x0=4
综上在x轴上存在定点N(4,0),使得∠PNM=∠QNM…(12分)
点评:本题考查椭圆的几何性质与标准方程,考查直线与椭圆的位置关系,考查韦达定理的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、函数的极大值大于函数的极小值 |
| B、若f′(x0)=0,则x0为函数f(x)的极值点 |
| C、函数的最值一定是极值 |
| D、在闭区间上的连续函数一定存在最值 |
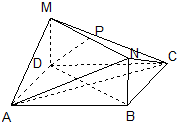 在如图所示的几何体中,四边形ABCD和BDMN都是矩形,且MD⊥平面ABCD,P是MN的中点.若AB=4,BC=3,MD=1,
在如图所示的几何体中,四边形ABCD和BDMN都是矩形,且MD⊥平面ABCD,P是MN的中点.若AB=4,BC=3,MD=1,
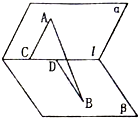 如图,在60°的两面角α-l-β中,A∈α,B∈β,AC⊥l与C,BD⊥l于D,AC=2,BD=3,AB=5,则CD=
如图,在60°的两面角α-l-β中,A∈α,B∈β,AC⊥l与C,BD⊥l于D,AC=2,BD=3,AB=5,则CD=