题目内容
设z=
，若复数z为纯虚数（其中i是虚数单位），则实数a等于（ ）
| 1-ai |
| i |
| A、-1 | ||
| B、0 | ||
| C、1 | ||
D、
|
考点：复数的基本概念
专题：数系的扩充和复数
分析：由复数的除法运算化简为a+bi（a，b∈R）的形式，利用实部等于0求得a的值．
解答：
解：∵z=
=
=-a-i，
由z为纯虚数，则-a=0，即a=0．
故选：B．
| 1-ai |
| i |
| (1-ai)•(-i) |
| -i2 |
由z为纯虚数，则-a=0，即a=0．
故选：B．
点评：本题考查复数的基本概念，考查了复数代数形式的除法运算，是基础题．
练习册系列答案
冲刺100分单元优化练考卷系列答案
相关题目
下列说法正确的是（ ）
| A、一个命题的逆命题为真，则它的逆否命题一定为真 |
| B、若a+b＞3，则a＞1或b＞2 |
| C、命题“所有的矩形都是正方形”的否命题和命题的否定均为真命题 |
| D、“a2+b2=0，则a，b全为0”的逆否命题是“若a，b全不为0，则a2+b2≠0” |
在下列命题
①?x∈R，(
)x＞0；
②“α=
”是“sinα=1”的充要条件；
③(
+
)4展开式中的常数项为2；
④设随机变量ξ～N（0，1），若P（ξ≥1）=p，则P（-1＜ξ＜0）=
-p．
其中所有正确命题的序号是（ ）
①?x∈R，(
| 1 |
| 2 |
②“α=
| π |
| 2 |
③(
| x3 |
| 2 |
| 1 |
| x |
④设随机变量ξ～N（0，1），若P（ξ≥1）=p，则P（-1＜ξ＜0）=
| 1 |
| 2 |
其中所有正确命题的序号是（ ）
| A、①②③ | B、①③④ |
| C、①②④ | D、②③④ |
在5×5的棋盘中，放入3颗黑子和2颗白子，它们均不在同一行且不在同一列，则不同的排列方法种数为（ ）
| A、150 | B、200 |
| C、600 | D、1200 |
下列说法正确的是（ ）
| A、函数的极大值大于函数的极小值 |
| B、若f′（x0）=0，则x0为函数f（x）的极值点 |
| C、函数的最值一定是极值 |
| D、在闭区间上的连续函数一定存在最值 |
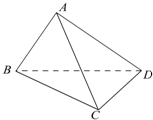在四面体ABCD中，△ABC与△DBC都是边长为4的正三角形．