题目内容
设双曲线M：
-
=1（a＞0，b＞0）的半焦距为c，且双曲线M与圆x2+y2=c2相交于A，B，C，D四点，若以A，B，C，D为顶点的四边形为正方形，则双曲线M的离心率等于（ ）
| x2 |
| a2 |
| y2 |
| b2 |
A、2+
| ||||
B、
| ||||
C、
| ||||
D、
|
考点：双曲线的简单性质
专题：计算题,直线与圆,圆锥曲线的定义、性质与方程
分析：由双曲线方程和圆的方程联立，求出交点，再由正方形的概念可得有AB=AD，即AB2=AD2，再由离心率公式，计算即可得到．
解答：
解：由双曲线的方程和圆x2+y2=c2联立，
可得x2=
=
，y2=
=
，
由于以A（x，y），B（-x，y），C（-x，-y），D（x，-y）
为顶点的四边形为正方形ABCD，
则有AB=AD，即为AB2=AD2，
即有4x2=4y2，
即为a2（2c2-a2）=（c2-a2）2，
化简即有c4-4a2c2+2a4=0，
e4-4e2+2=0，
e2=2±
，
由于e＞1，则e=
．
故选B．
可得x2=
| c4-b4 |
| c2 |
| a2(2c2-a2) |
| c2 |
| b4 |
| c2 |
| (c2-a2)2 |
| c2 |
由于以A（x，y），B（-x，y），C（-x，-y），D（x，-y）
为顶点的四边形为正方形ABCD，
则有AB=AD，即为AB2=AD2，
即有4x2=4y2，
即为a2（2c2-a2）=（c2-a2）2，
化简即有c4-4a2c2+2a4=0，
e4-4e2+2=0，
e2=2±
| 2 |
由于e＞1，则e=
2+
|
故选B．
点评：本题考查双曲线方程和圆方程联立求交点的方法，考查离心率的求法，考查运算能力，属于基础题．
练习册系列答案
相关题目
甲乙两人从4门课程中各选修两门，则甲乙所选的课程中至少有1门不相同的选法共有（ ）种．
| A、30 | B、36 | C、60 | D、72 |
若双曲线
-
=1（a＞0，b＞0）的一条渐近线为y=
x，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
A、
| ||
| B、2 | ||
C、
| ||
D、
|
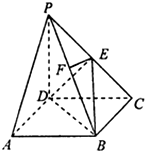如图，在四棱锥P-ABCD中，底面ABCD是正方形，侧棱PD⊥底面ABCD，PD=DC，E是PC的中点，作EF⊥PB，垂足为F．
在植物活动前为保证树苗的质量，林管部门会对树苗进行检测．先从甲、乙两种树苗中各抽测了10株树苗的高度，量出的高度（单位：厘米）制作成茎叶图如下，甲，乙两种树苗的平均高度分别记为| x |
| y |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知sin（π+α）=
，α为第三象限角，则tanα=（ ）
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|