题目内容
设命题p:|4x-3|≤1,命题q:x2-(2a+1)x+a(a+1)≤0,若p是q的充分不必要条件,求实数a的取值范围.
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:求解出命题p:
≤x≤1,命题q:a≤x≤a+1,根据p是q的充分不必要条件,得出
即可求解.
| 1 |
| 2 |
|
解答:
解:∵命题p:|4x-3|≤1,
∴
≤x≤1,
∵命题q:x2-(2a+1)x+a(a+1)≤0,
∴a≤x≤a+1,
∵若p是q的充分不必要条件,
∴
即0≤a≤
故实数a的取值范围:0≤a≤
∴
| 1 |
| 2 |
∵命题q:x2-(2a+1)x+a(a+1)≤0,
∴a≤x≤a+1,
∵若p是q的充分不必要条件,
∴
|
| 1 |
| 2 |
故实数a的取值范围:0≤a≤
| 1 |
| 2 |
点评:本题考查充分必要条件的定义,不等式的求解,属于中档题.

练习册系列答案
相关题目
在R上定义的函数f(x)是偶函数,且f(x)=f(2-x),若f(x)在区间x∈[1,2)是减函数,则函数 f(x)( )
| A、在区间[-2,-1]上是减函数,区间[3,4]上是增函数 |
| B、在区间[-2,-1]上是减函数,区间[3,4]上是减函数 |
| C、在区间[-2,-1]上是增函数,区间[3,4]上是增函数 |
| D、在区间[-2,-1]上是增函数,区间[3,4]上是减函数 |
点M(x,y)在函数y=-2x+8的图象上,当x∈[2,5]时,
的取值范围是( )
| y+1 |
| x+1 |
A、[-
| ||||
B、[0,
| ||||
C、[-
| ||||
| D、[2,4] |
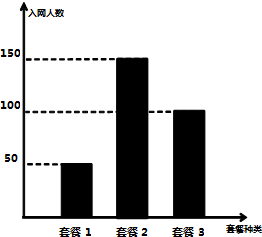 移动公司在国庆期间推出4G套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元.国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率.
移动公司在国庆期间推出4G套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元.国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率.