题目内容
设椭圆C:
+
=1(a>b>0)的离心率为e=
,M是椭圆C上的一点,且点M到椭圆C两焦点的距离之和为4.
(1)求椭圆C的方程;
(2)过椭圆C的左顶点A的直线l交椭圆于另一点B,P(0,t)是y轴上一点,满足|PA|=|PB|,
•
=4,求实数t的值.
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 2 |
(1)求椭圆C的方程;
(2)过椭圆C的左顶点A的直线l交椭圆于另一点B,P(0,t)是y轴上一点,满足|PA|=|PB|,
| PA |
| PB |
考点:椭圆的简单性质
专题:平面向量及应用,圆锥曲线的定义、性质与方程
分析:(1)根据椭圆的定义与离心率求出b2与a2,得椭圆C的标准方程;
(2)由题意得P是线段AB垂直平分线上的点,讨论AB⊥y轴和AB与y轴不垂直时,求出t的值.
(2)由题意得P是线段AB垂直平分线上的点,讨论AB⊥y轴和AB与y轴不垂直时,求出t的值.
解答:
解:(1)根据题意得,2a=4,∴a=2;
又∵e=
=
,∴c=
;
∴b2=a2-c2=4-3=1,
∴椭圆C的方程为
+y2=1;
(2)∵P(0,t)是y轴上一点,且|PA|=|PB|,
∴P是线段AB垂直平分线上的点;
∴①当AB⊥y轴时,A(-2,0),B(2,0),
则
=(-2,-t),
=(2,-t);
∴
•
=-4+t2=4,
解得t=±2
;
②当AB与y轴不垂直时,设B(x1,y1)(y1≠0),∴AB的中点为(
,
),
则线段AB的垂直平分线方程为y-
=-
(x-
),
令x=0,则t=
=-
y1,
∴
=(-2,
y1),
=(x1,
y1),
∴
•
=-2x1+
y12=-2x1+
•
=4,
∴x1=-
或x1=-2(舍去),
∴y12=
=
,
∴y1=±
,
∴t=±
,
综上,t的值为±2
或±
.
又∵e=
| c |
| a |
| ||
| 2 |
| 3 |
∴b2=a2-c2=4-3=1,
∴椭圆C的方程为
| x2 |
| 4 |
(2)∵P(0,t)是y轴上一点,且|PA|=|PB|,
∴P是线段AB垂直平分线上的点;
∴①当AB⊥y轴时,A(-2,0),B(2,0),
则
| PA |
| PB |
∴
| PA |
| PB |
解得t=±2
| 2 |
②当AB与y轴不垂直时,设B(x1,y1)(y1≠0),∴AB的中点为(
| x1-2 |
| 2 |
| y1 |
| 2 |
则线段AB的垂直平分线方程为y-
| y1 |
| 2 |
| x1+2 |
| y1 |
| x1-2 |
| 2 |
令x=0,则t=
| x12-4+y12 |
| 2y1 |
| 3 |
| 2 |
∴
| PA |
| 3 |
| 2 |
| PB |
| 5 |
| 2 |
∴
| PA |
| PB |
| 15 |
| 4 |
| 15 |
| 4 |
| 4-x12 |
| 4 |
∴x1=-
| 2 |
| 15 |
∴y12=
| 4-x12 |
| 4 |
| 224 |
| 225 |
∴y1=±
4
| ||
| 15 |
∴t=±
2
| ||
| 5 |
综上,t的值为±2
| 2 |
2
| ||
| 5 |
点评:本题考查了椭圆的方程,也考查了直线与椭圆的位置关系,考查了分类讨论的数学思想,考查向量的数量积公式,是难题.

练习册系列答案
 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
△ABC的内角A,B,C的对边分别为a,b,c,若a,b,c成等比数列,且c=2a,则sinB=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知θ∈(0,
),则
+
的最小值为( )
| π |
| 2 |
| 2 |
| sinθ |
| 3 |
| 1-sinθ |
A、5+2
| ||
| B、10 | ||
C、6+2
| ||
D、6+5
|
在△ABC中,M是BC的中点,AM=5,BC=6,则
•
等于( )
| AB |
| AC |
| A、9 | B、12 | C、16 | D、30 |
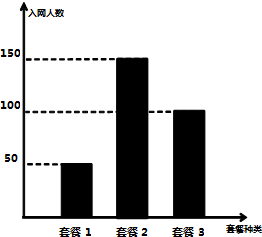 移动公司在国庆期间推出4G套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元.国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率.
移动公司在国庆期间推出4G套餐,对国庆节当日办理套餐的客户进行优惠,优惠方案如下:选择套餐一的客户可获得优惠200元,选择套餐二的客户可获得优惠500元,选择套餐三的客户可获得优惠300元.国庆节当天参与活动的人数统计结果如图所示,现将频率视为概率.