题目内容
已知函数f(x)=lnx- (m∈R)在区间[1,e]上取得最小值4,则m=________.
(m∈R)在区间[1,e]上取得最小值4,则m=________.
-3e
[解析] f ′(x)= (x>0),
(x>0),
当m>0时,f ′(x)>0,f(x)在区间[1,e]上为增函数,
f(x)有最小值f(1)=-m=4,
得m=-4,与m>0矛盾.
当m<0时,若-m<1即m>-1,f(x)min=f(1)=-m=4,
得m=-4,与m>-1矛盾;
若-m∈[1,e],即-e≤m≤-1,f(x)min=f(-m)=ln(-m)+1=4,
解得m=-e3,与-e≤m≤-1矛盾;
若-m>e,即m<-e时,f(x)min=f(e)=1- =4,解得m=-3e,符合题意.
=4,解得m=-3e,符合题意.

练习册系列答案
相关题目
 B.±
B.±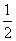 D.
D.
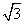 |b|,若函数f(x)=
|b|,若函数f(x)=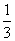 x3+|a|x2+2a·bx+1在R上有极值,则〈a,b〉的取值范围是( )
x3+|a|x2+2a·bx+1在R上有极值,则〈a,b〉的取值范围是( ) ] B.(0,
] B.(0, ]
]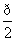 ] D.(
] D.( 和
和 R B.
R B. R和
R和 R
R R和
R和 R D.以上都不对
R D.以上都不对 +xlnx,g(x)=x3-x2-x-1.
+xlnx,g(x)=x3-x2-x-1. ,2],都有f(s)≥g(t)成立,求实数a的取值范围.
,2],都有f(s)≥g(t)成立,求实数a的取值范围.
 ,
,
 ,则向量
,则向量