题目内容
5．在等差数列{an}中，已知a4=-15，公差d=3，则数列{an}的前n项和Sn的最小值为-108．分析 求出首项a4=-24，公差d=3，从而得到Sn=$\frac{3}{2}$（n-$\frac{17}{2}$）2-$\frac{867}{8}$，由此能求出数列{an}的前n项和Sn的最小值．
解答 解：∵等差数列{an}中，a4=-15，公差d=3，
∴a1=a4-3d=-15-9=-24，
∴Sn=-24n+$\frac{n（n-1）}{2}×3$=$\frac{3}{2}$（n-$\frac{17}{2}$）2-$\frac{867}{8}$，
∴n=8或n=9时，
数列{an}的前n项和Sn取最小值S8=S9=-108．
故答案为：-108．
点评 本题考查等差数列的前n项和的最小值的求法，是基础题，解题时要认真审题，注意等差数列的性质的合理运用．
练习册系列答案
培优三好生系列答案
优化作业上海科技文献出版社系列答案
相关题目
11．若复数2-bi（b∈R）的实部与虚部之和为零，则b的值为（ ）
| A． | 2 | B． | $\frac{2}{3}$ | C． | -$\frac{2}{3}$ | D． | -2 |
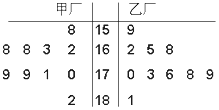某企业有两个分厂生产某种零件，按规定内径尺寸（单位：mm）的数据落在（164，181]的零件为优质品．现从两个分厂生产的零件中随机各抽出10件，量其内径尺寸（单位：mm），获得内径尺寸数据的茎叶图如图所示．
10．已知sinαcosβ=1，则cos（α+β）的值是（ ）
| A． | 0 | B． | 1 | C． | -1 | D． | ±1 |
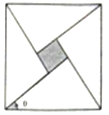我国古代数学家赵爽利用“勾股圈方图”巧妙的证明了勾股定理，成就了我国古代数学的骄傲，后人称之为“赵爽弦图”．他是由四个全等的直角三角形和中间的一个小正方形拼成的一个大正方形，若直角三角形中较小的锐角记为θ，大正方形的面积为25，小正方形的面积为1，则$sin\frac{θ}{2}+cos\frac{θ}{2}$=$\frac{{2\sqrt{10}}}{5}$．
14．命题“?x0∈R，${x_0}^2-{x_0}-1＞0$”的否定是（ ）
| A． | ?x∈R，x2-x-1≤0 | B． | ?x∈R，x2-x-1＞0 | ||
| C． | ?x0∈R，${x_0}^2-{x_0}-1≤0$ | D． | ?x0∈R，${x_0}^2-{x_0}-1≥0$ |