题目内容
已知双曲线Γ的焦点为(0,-2)和(0,2),离心率为
,过双曲线Γ的上支上一点P作双曲线Γ的切线交两条渐近线分别于点A,B(A,B在x轴上方).
(1)求双曲线Γ的标准方程;
(2)探究
•
是否为定值,若是,求出该定值,若不是,说明理由.
2
| ||
| 3 |
(1)求双曲线Γ的标准方程;
(2)探究
| OA |
| OB |
考点:双曲线的简单性质
专题:平面向量及应用,直线与圆,圆锥曲线的定义、性质与方程
分析:(1)依题意可设双曲线的标准方程为
-
=1(a>0,b>0),由c=2,
=
,b2=c2-a2,解出a,b,即可得到双曲线方程;
(2)
•
是定值2.设出直线AB的方程,联立双曲线方程,消去y,由判别式为0,可得k2+b2=3,再由双曲线的渐近线方程和直线AB的方程联立,可得A,B的横坐标之积和纵坐标之积,结合向量的数量积的坐标表示,计算即可得到定值.
| y2 |
| a2 |
| x2 |
| b2 |
| c |
| a |
2
| ||
| 3 |
(2)
| OA |
| OB |
解答:
解:(1)依题意可设双曲线的标准方程为
-
=1(a>0,b>0),
∵c=2,
=
,b2=c2-a2,∴a=
,b=1,
∴双曲线的标准方程为
-x2=1.
(2)
•
是定值2,理由如下:
设直线AB:y=kx+b(b>0),
由
得(k2-3)x2+2kbx+b2-3=0,
则k2-3≠0,△=(2kb)2-4(k2-3)(b2-3)=0,
解得k2+b2=3,
设A(x1,y1),B(x2,y2),则y1>0,y2>0,
由双曲线渐近线方程:y2-3x2=0与y=kx+b联立,
得 (k2-3)x2+2kbx+b2=0,
则k2-3≠0,△=(2kb)2-4(k2-3)b2>0,
则x1x2=
=
=-1,y1y2=3|x1x2|=3,
∴
•
=x1x2+y1y2=-1+3=2.
| y2 |
| a2 |
| x2 |
| b2 |
∵c=2,
| c |
| a |
2
| ||
| 3 |
| 3 |
∴双曲线的标准方程为
| y2 |
| 3 |
(2)
| OA |
| OB |
设直线AB:y=kx+b(b>0),
由
|
则k2-3≠0,△=(2kb)2-4(k2-3)(b2-3)=0,
解得k2+b2=3,
设A(x1,y1),B(x2,y2),则y1>0,y2>0,
由双曲线渐近线方程:y2-3x2=0与y=kx+b联立,
得 (k2-3)x2+2kbx+b2=0,
则k2-3≠0,△=(2kb)2-4(k2-3)b2>0,
则x1x2=
| b2 |
| k2-3 |
| 3-k2 |
| k2-3 |
∴
| OA |
| OB |
点评:本题考查双曲线的方程和性质,主要考查联立直线方程和双曲线方程,消去未知数,运用判别式和韦达定理,同时考查向量的数量积的坐标表示,考查运算能力,属于中档题和易错题.

练习册系列答案
相关题目
已知函数f(x)=
,若|f(x)|≥a(x-1),则a的取值范围是( )
|
| A、(-∞,-1] |
| B、(-∞,1] |
| C、[-1,1] |
| D、[-1,0] |
直角坐标系xoy中,以原点为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的极坐标方程为ρ=2sinθ,直线l的参数方程为
(t为参数),则圆C截直线l所得的弦长为( )
|
| A、1 | ||
B、
| ||
| C、2 | ||
D、2
|
我国发射的“嫦娥一号”探月卫星的运行轨道分为三个阶段,绕地阶段、变轨阶段、绕月阶段,绕地阶段时以地球中心F2为焦点的椭圆,近地点A距离地面为m千米,远地点B距离地面为n千米,地球的半径为R千米,则卫星运行轨道的短轴长为( )
A、2
| ||
B、
| ||
| C、mn | ||
| D、2mn |
下列结论中正确的是( )
| A、“x≠1”是“x(x-1)≠0”的充分不必要条件 |
| B、已知随机变量ξ服从正态分布N(5,1),且P(4≤ξ≤6)=0.7,则P(ξ>6)=0.15 |
| C、将一组数据中的每个数据都减去同一个数后,平均数与方差均没有变化 |
| D、某单位有职工750人,其中青年职工350人,中年职工250人,老年职工150人.为了解该单位职工的健康情况,应采用系统抽样的方法从中抽取样本 |
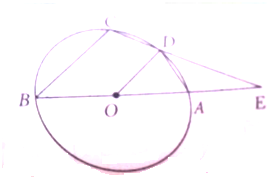 如图,BA是⊙O的直径,延长BA至E,使得AE=AO,过E点作⊙O的割线交⊙O于D、C,使得AD=DC.
如图,BA是⊙O的直径,延长BA至E,使得AE=AO,过E点作⊙O的割线交⊙O于D、C,使得AD=DC. 在等腰直角三角形ABC中,AB=AC=1,点P是边AB上异于A、B的一点,光线从点P出发,经BC、CA反射后又回到点P(如图所示),若光线QR经过△ABC的重心,则AP=( )
在等腰直角三角形ABC中,AB=AC=1,点P是边AB上异于A、B的一点,光线从点P出发,经BC、CA反射后又回到点P(如图所示),若光线QR经过△ABC的重心,则AP=( )