题目内容
给出函数①y=x3cosx,②y=sin2x,③y=|x2-x|,④y=ex-e-x,其中是奇函数的是( )
| A、①② | B、①④ | C、②④ | D、③④ |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据奇偶函数定义判断,首项确定定义域,判定其定义域是否关于原点对称,再判定f(x)与f(-x)的关系.
解答:
解:判断①②③④定义域都为R,关于原点对称,
①y=x3cosx,f(x)=x3cosx,f(-x)=-x3cosx,
∴f(-x)=-f(x),
∴①是奇函数,
②y=sin2x,
f(x)=sin2x,f(-x)=sin2(-x)=[-sinx]2=sin2x
∴f(-x)=f(x),
∴②偶函数
③y=|x2-x|,f(x)=|x2-x|,f(-x)=|(-x)2+x|=|x2+x|
∴f(-x)≠-f(x),f(-x)≠f(x),
∴③不是奇函数也不是偶函数.
④y=ex-e-x,
f(x)=ex-e-x,f(-x)═e-x-ex=-[ex-e-x]=-f(x)
④是奇函数,
①y=x3cosx,f(x)=x3cosx,f(-x)=-x3cosx,
∴f(-x)=-f(x),
∴①是奇函数,
②y=sin2x,
f(x)=sin2x,f(-x)=sin2(-x)=[-sinx]2=sin2x
∴f(-x)=f(x),
∴②偶函数
③y=|x2-x|,f(x)=|x2-x|,f(-x)=|(-x)2+x|=|x2+x|
∴f(-x)≠-f(x),f(-x)≠f(x),
∴③不是奇函数也不是偶函数.
④y=ex-e-x,
f(x)=ex-e-x,f(-x)═e-x-ex=-[ex-e-x]=-f(x)
④是奇函数,
点评:本题综合考查了奇偶函数的定义,注意定义域的限制,定义式的运用,属于中档题.

练习册系列答案
相关题目
已知函数f(x)=
,若|f(x)|≥a(x-1),则a的取值范围是( )
|
| A、(-∞,-1] |
| B、(-∞,1] |
| C、[-1,1] |
| D、[-1,0] |
不等式|x+2a|+|x-a|≥3对任意实数x都成立,则实数a的取值范围是( )
| A、(-∞,-3]∪[3,+∞) |
| B、(-∞,-1]∪[1,+∞) |
| C、[-3,3] |
| D、[-1,1] |
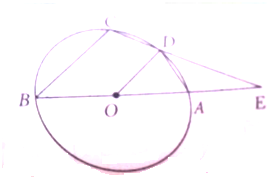 如图,BA是⊙O的直径,延长BA至E,使得AE=AO,过E点作⊙O的割线交⊙O于D、C,使得AD=DC.
如图,BA是⊙O的直径,延长BA至E,使得AE=AO,过E点作⊙O的割线交⊙O于D、C,使得AD=DC.