题目内容
已知抛物线C顶点在原点,焦点F在x轴上,抛物线C上的点(1,m)到F的距离等于2.
(1)求抛物线C的方程;
(2)若不与x轴垂直的直线l1与抛物线C交于A、B两点,且线段AB的垂直平分线l2恰好过点M(4,0),求证:线段AB中点的横坐标为定值.
(1)求抛物线C的方程;
(2)若不与x轴垂直的直线l1与抛物线C交于A、B两点,且线段AB的垂直平分线l2恰好过点M(4,0),求证:线段AB中点的横坐标为定值.
考点:抛物线的简单性质
专题:圆锥曲线的定义、性质与方程
分析:(1)由题意设出抛物线方程,把点(1,m)到F的距离等于2转化为点到准线的距离等于2求得p的值,则抛物线方程可求;
(2)设线段AB中点的坐标为N(x0,y0),A(x1,y1),B(x2,y2),求出直线MN的斜率,得到直线AB的斜率,写出直线AB的方程,和抛物线方程联立后由根与系数关系求得即线段AB中点的横坐标为定值2.
(2)设线段AB中点的坐标为N(x0,y0),A(x1,y1),B(x2,y2),求出直线MN的斜率,得到直线AB的斜率,写出直线AB的方程,和抛物线方程联立后由根与系数关系求得即线段AB中点的横坐标为定值2.
解答:
(1)解:由题意设抛物线方程为y2=2px,其准线方程为x=-
,
∵(1,m)到焦点的距离等于到其准线的距离,
∴1+
=2,p=2.
∴此抛物线的方程为y2=4x;
(2)证明:设线段AB中点的坐标为N(x0,y0),A(x1,y1),B(x2,y2),
则直线MN的斜率为
,
∵AB不垂直于x轴,∴直线AB的斜率为
,直线AB的方程为y-y0=
(x-x0),
联立方程
消去x,得(1-
)y2-y0y+y02+x0(x0-4)=0,
∴y1+y2=
,
∵N为AB中点,∴
=y0,即
=y0,
∴x0=2,即线段AB中点的横坐标为定值2.
| p |
| 2 |
∵(1,m)到焦点的距离等于到其准线的距离,
∴1+
| p |
| 2 |
∴此抛物线的方程为y2=4x;
(2)证明:设线段AB中点的坐标为N(x0,y0),A(x1,y1),B(x2,y2),
则直线MN的斜率为
| y0 |
| x0-4 |
∵AB不垂直于x轴,∴直线AB的斜率为
| 4-x0 |
| y0 |
| 4-x0 |
| y0 |
联立方程
|
| x0 |
| 4 |
∴y1+y2=
| 4y0 |
| 4-x0 |
∵N为AB中点,∴
| y1+y2 |
| 2 |
| 2y0 |
| 4-x0 |
∴x0=2,即线段AB中点的横坐标为定值2.
点评:本题考查了抛物线的简单几何性质,考查了直线与圆锥曲线的关系,训练了“设而不求”的解题思想方法,是中档题.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目
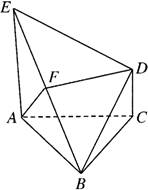 已知:△ABC是正三角形,EA、CD垂直平面ABC,且EA=AB=2,DC=1,F是BE中点.求证:(1)FD∥平面ABC;
已知:△ABC是正三角形,EA、CD垂直平面ABC,且EA=AB=2,DC=1,F是BE中点.求证:(1)FD∥平面ABC;