题目内容
6.已知函数f(x)=$\frac{x+1}{{e}^{x}-1}$+x(x∈(0,+∞),且f(x)在x0处取得最小值,则以下各式正确的序号为( )①f(x0)<x0+1 ②f(x0)=x0+1 ③f(x0)>x0+1 ④f(x0)<3 ⑤f(x0)>3.
| A. | ①④ | B. | ②④ | C. | ②⑤ | D. | ③⑤ |
分析 求导数,利用最小值点且为极小值点,即可判断①②③;利用g(x)=ex-x-2,x>0,的零点,由零点判定定理可判断④⑤.
解答 解:函数f(x)=$\frac{x+1}{{e}^{x}-1}$+x(x∈(0,+∞),
可得f′(x)=$\frac{-1-x{e}^{x}}{({e}^{x}-1)^{2}}$+1=$\frac{{e}^{x}({e}^{x}-x-2)}{({e}^{x}-1)^{2}}$,
由f(x)在x0处取得最小值,也为极小值.
即有f′(x0)=0,即ex0=x0+2,
f(x0)=$\frac{{x}_{0}+1}{{e}^{{x}_{0}}-1}$+x0=1+x0,
即①,③错误,②正确;
令g(x)=ex-x-2,x>0,
则g(1)=e-1-2=e-3<0,
g(2)=e2-4>0,
则g(x)的零点介于(1,2),
则x0<2,f(x0)=1+x0<3,
故④正确,⑤错误.
即有②④正确.
故选:B.
点评 本题考查导数知识的应用:求最值,考查函数零点判定定理的运用,考查学生分析解决问题的能力,有难度.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
3.已知tanα=$\frac{1}{2}$,tanβ=-$\frac{1}{3}$,则$\frac{3sinαcosβ-sinβcosα}{cosαcosβ+2sinαsinβ}$=( )
| A. | $\frac{7}{8}$ | B. | $\frac{11}{8}$ | C. | $\frac{7}{4}$ | D. | $\frac{11}{4}$ |
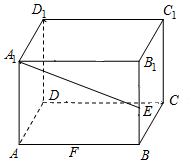 已知在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点F是AB边上动点,点E是棱B1B的中点.
已知在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点F是AB边上动点,点E是棱B1B的中点.