题目内容
6.已知g(x)=sin2x,将g(x)的图象向左平移$\frac{π}{8}$个单位长度,再将图象上各点的横坐标缩短到原来的$\frac{1}{4}$,得到函数f(x)的图象,则( )| A. | $f(x)=sin(8x-\frac{π}{4})$ | B. | $f(x)=sin(8x+\frac{π}{4})$ | C. | $f(x)=sin(\frac{x}{2}-\frac{π}{4})$ | D. | $f(x)=sin(\frac{x}{2}+\frac{π}{4})$ |
分析 利用函数y=Asin(ωx+φ)的图象变换规律,得出结论.
解答 解:将g(x)=sin2x的图象向左平移$\frac{π}{8}$个单位长度,可得y=sin2(x+$\frac{π}{8}$)=sin(2x+$\frac{π}{4}$)的图象;
再将图象上各点的横坐标缩短到原来的$\frac{1}{4}$,得到函数f(x)=sin(8x+$\frac{π}{4}$)的图象,
故选:B.
点评 本题主要考查函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
相关题目
19.已知$\frac{sinx+1}{cosx}=\frac{1}{2}$,则$\frac{sinx-1}{cosx}$的值是( )
| A. | $\frac{1}{2}$ | B. | 2 | C. | $-\frac{1}{2}$ | D. | -2 |
14.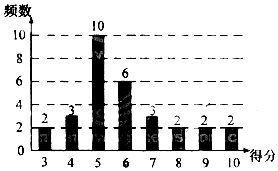 为了普及环保知识,增强环保意识,某大学随即抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为m,众数为n,平均值为$\overline{x}$,则( )
为了普及环保知识,增强环保意识,某大学随即抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为m,众数为n,平均值为$\overline{x}$,则( )
 为了普及环保知识,增强环保意识,某大学随即抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为m,众数为n,平均值为$\overline{x}$,则( )
为了普及环保知识,增强环保意识,某大学随即抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分值的中位数为m,众数为n,平均值为$\overline{x}$,则( )| A. | m=n=$\overline{x}$ | B. | m=n<$\overline{x}$ | C. | m<n<$\overline{x}$ | D. | n<m<$\overline{x}$ |
1.$sin\frac{17π}{4}$=( )
| A. | $\frac{{\sqrt{2}}}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | $-\frac{{\sqrt{3}}}{2}$ |
11.已知m,n是两条不同直线α,β是两个不同平面,则下列命题正确的是( )
| A. | 若α,β垂直于同一平面,则α与β平行 | |
| B. | 若m,n平行于同一平面,则m与n平行 | |
| C. | 若m,n不平行,则m与n不可能垂直于同一平面 | |
| D. | 若α,β不平行,则在α内不存在与β平行的直线 |
15.已知复数z=3-4i(i是虚数单位),则复数$\frac{\overline z}{1+i}$的虚部为( )
| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}i$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}i$ |