题目内容
5.设双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右顶点为A,P为双曲线上的一个动点(不是顶点),若从点A引双曲线的两条渐近线的平行线,与直线OP分别交于Q、R两点,其中O为坐标原点,则|OP|2与|OQ|•|OR|的大小关系为|OP|2=|OQ|•|OR|.(填“>”,“<”或“=”)分析 先求出A的坐标和渐近线方程,设OP的方程为y=kx,AR的方程为y=$\frac{b}{a}$(x-a),求得$\overrightarrow{OR}$、$\overrightarrow{OQ}$的坐标,计算|$\overrightarrow{OQ}$•$\overrightarrow{OR}$|的值,把双曲线方程与直线OP方程联立解得|$\overrightarrow{OP}$|2,比较可得结论.
解答 解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1({a>0,b>0})$的右顶点为A(a,0),
渐近线方程为y=±$\frac{b}{a}$x,
设OP的方程为y=kx,AR的方程为y=$\frac{b}{a}$(x-a),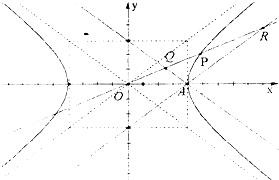
解得$\overrightarrow{OR}$=(-$\frac{ab}{ak-b}$,-$\frac{kab}{ak-b}$),
同理可得$\overrightarrow{OQ}$=($\frac{ab}{ak+b}$,$\frac{kab}{ak+b}$).
∴|$\overrightarrow{OQ}$•$\overrightarrow{OR}$|=|$\frac{ab}{ak+b}$•(-$\frac{ab}{ak-b}$)+$\frac{kab}{ak+b}$•(-$\frac{kab}{ak-b}$)|
=$\frac{{a}^{2}{b}^{2}(1+{k}^{2})}{|{a}^{2}{k}^{2}-{b}^{2}|}$.
设$\overrightarrow{OP}$=(m,n),则由双曲线方程与直线OP方程联立解得:m2=$\frac{{a}^{2}{b}^{2}}{{b}^{2}-{a}^{2}{k}^{2}}$,n2=$\frac{{k}^{2}{a}^{2}{b}^{2}}{{b}^{2}-{a}^{2}{k}^{2}}$,
∴|$\overrightarrow{OP}$|2=m2+n2=$\frac{(1+{k}^{2}){a}^{2}{b}^{2}}{{b}^{2}-{a}^{2}{k}^{2}}$,
∵点P在双曲线上,∴b2-a2k2>0,
无论点P在什么位置,总有|$\overrightarrow{OP}$|2=|$\overrightarrow{OQ}$•$\overrightarrow{OR}$|═|$\overrightarrow{OQ}$|•|$\overrightarrow{OR}$|.
即为|OP|2=|OQ|•|OR|.
故答案为:=.
点评 本题考查双曲线的方程、性质及应用,考查转化思想,运用两个向量的数量积的坐标表示,式子的变形、化简是解题的难点,属于中档题.

 优等生题库系列答案
优等生题库系列答案| A. | -$\frac{1}{2}$ | B. | $\frac{1}{2}i$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{2}i$ |
①AC⊥BD;②△ADC是正三角形;③AB与CD成60°角;④AB与平面BCD成60°角.
则其中正确结论的个数是( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
| A. | 存在满足x<y的x,y∈[a,b]使得f(x)>f(y) | |
| B. | 不存在x,y∈[a,b]满足x<y且f(x)≤f(y) | |
| C. | 对任意满足x<y的x,y∈[a,b]都有f(x)>f(y) | |
| D. | 存在满足x<y的x,y∈[a,b]都有f(x)≤f(y) |
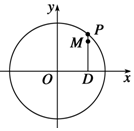 如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为线段PD上一点,且$|{DP}|=\sqrt{2}|{DM}|$.
如图,设P是圆x2+y2=6上的动点,点D是P在x轴上的投影,M为线段PD上一点,且$|{DP}|=\sqrt{2}|{DM}|$.