题目内容
9.已知函数f(x)=$\frac{1}{a-x(1-x)}$的值恒小于1,则实数a的取值范围是( )| A. | (-∞,$\frac{1}{4}$)∪($\frac{5}{4}$,+∞) | B. | (-∞,$\frac{1}{4}$) | C. | ($\frac{5}{4}$,+∞) | D. | 以上都不对 |
分析 根据题意可得a-x(1-x)<0或a-x(1-x)>1恒成立,分类讨论,根据二次函数的性质即可判断.
解答 解:∵f(x)=$\frac{1}{a-x(1-x)}$的值恒小于1,
∴$\frac{1}{a-x(1-x)}$<1,
∴a-x(1-x)<0或a-x(1-x)>1,
对于a-x(1-x)<0,即a<x-x2=-(x-$\frac{1}{2}$)2+$\frac{1}{4}$,故无论a取何值,不等式不可能恒成立,
对于a-x(1-x)>1,即a>1+x-x2=-(x-$\frac{1}{2}$)2+$\frac{5}{4}$,故a>$\frac{5}{4}$,
综上所述a的取值范围为($\frac{5}{4}$,+∞),
故选:C.
点评 本题考查了二次函数的最值和函数恒成立的问题,属于中档题.

练习册系列答案
相关题目
19.已知实数x,y满足约束条件$\left\{\begin{array}{l}x≥0\\ x-y≤0\\ x+y≤a\end{array}\right.({a>0})$,若z=x+ay的最大值为2,则$m+\frac{a^2}{{m-\sqrt{2}}}({m>\sqrt{2}})$的最小值为( )
| A. | $\sqrt{2}$ | B. | $2\sqrt{2}$ | C. | $3\sqrt{2}$ | D. | 6 |
4.阅读如图所示的程序框图,则输出的S的值是( )


| A. | $\frac{8}{9}$ | B. | $\frac{9}{10}$ | C. | $\frac{7}{8}$ | D. | $\frac{6}{7}$ |
14.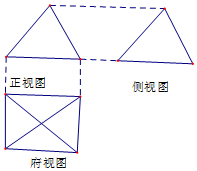 如图,一个简单空间几何体的三视图与侧视图都是边长为2的正三角形,俯视图是正方形,则此几何体的侧面积是( )
如图,一个简单空间几何体的三视图与侧视图都是边长为2的正三角形,俯视图是正方形,则此几何体的侧面积是( )
 如图,一个简单空间几何体的三视图与侧视图都是边长为2的正三角形,俯视图是正方形,则此几何体的侧面积是( )
如图,一个简单空间几何体的三视图与侧视图都是边长为2的正三角形,俯视图是正方形,则此几何体的侧面积是( )| A. | $4+4\sqrt{3}$ | B. | 8 | C. | $4\sqrt{3}$ | D. | 12 |
18.若二次函数y=x2+2x+(m+3)有两个不同的零点,则m的取值范围是( )
| A. | (-∞,-2) | B. | (-∞,-2] | C. | (-∞,4) | D. | (4,+∞) |
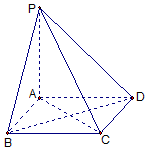 如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=AB=2.
如图,棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=AB=2.