题目内容
14．
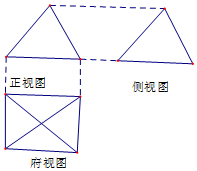如图，一个简单空间几何体的三视图与侧视图都是边长为2的正三角形，俯视图是正方形，则此几何体的侧面积是（ ）| A． | $4+4\sqrt{3}$ | B． | 8 | C． | $4\sqrt{3}$ | D． | 12 |
分析 根据已知中一个简单空间几何体的三视图中，其正视图与侧视图都是边长为2的正三角形，俯视图轮廓为正方形，我们可以判断出该几何体为一个正四棱锥，进而求出其底面棱长及侧高，代入棱棱侧面积公式，即可得到答案．
解答 解：由已知中几何体的三视图中，
正视图与侧视图都是边长为2的正三角形，俯视图轮廓为正方形
可得这个几何体是一个正四棱椎，
且底面的棱长为2，棱锥的高为$\sqrt{3}$，其侧高为2
则棱锥的侧面积S=4×$\frac{1}{2}$×2×2=8
故选B
点评 本题考查的知识点是由三视图求侧面积，其中根据已知中的三视图分析出几何体的形状及几何特征是解答本题的关键．
练习册系列答案
相关题目
4．已知△ABC中，角A、B、C所对的边长分别为a、b、c，且知A、B、C依次成等差数列，a+c=13，a2+c2=89，m为函数$y=\frac{{{x^2}+1}}{{\sqrt{{x^2}+1}}}$的最小值；椭圆E：的左右焦点为F1，F2，E上一点P到F1距离的最大值为b，最小值为m，则椭圆E的离心率的算术平方根为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{{\sqrt{2}}}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{1}{7}$ |
9．已知函数f（x）=$\frac{1}{a-x（1-x）}$的值恒小于1，则实数a的取值范围是（ ）
| A． | （-∞，$\frac{1}{4}$）∪（$\frac{5}{4}$，+∞） | B． | （-∞，$\frac{1}{4}$） | C． | （$\frac{5}{4}$，+∞） | D． | 以上都不对 |
19．如图，已知PA⊥平面ABC，∠ABC=120°，PA=AB=BC=6，$|{\overrightarrow{PC}}|$=等于（ ）
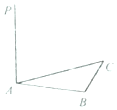
| A． | $6\sqrt{2}$ | B． | 6 | C． | 12 | D． | 144 |
4．双曲线$\frac{x^2}{8}-{y^2}=1$的焦点到其渐近线的距离是（ ）
| A． | $2\sqrt{2}$ | B． | 1 | C． | 2 | D． | $\sqrt{3}$ |