题目内容
已知函数f(x)=
x2+alnx,g(x)=(a+1)x,a≠-1.
(1)若函数f(x)在点(2,f(2))处的切线斜率为
,求f(x)的极值;
(2)若a∈(1,e],F(x)=f(x)-g(x),求证:当x1,x2∈[1,a]时,|F(x1)-F(x2)|<1恒成立.
| 1 |
| 2 |
(1)若函数f(x)在点(2,f(2))处的切线斜率为
| 1 |
| 2 |
(2)若a∈(1,e],F(x)=f(x)-g(x),求证:当x1,x2∈[1,a]时,|F(x1)-F(x2)|<1恒成立.
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由对数函数的定义得到函数的定义域为x大于0,求出f′(x),根据曲线在(2,f(2))处切线的斜率为
,得到f′(2)=
,代入导函数得到关于a的方程,求出a的解即得到函数的解析式,可令f′(x)=0求出x的值,在定义域内利用x的范围讨论导函数的正负即可得到函数的增减区间,利用函数的增减性得到函数的极值即可;
(2)求出函数f(x)在区间[1,a]上的最大值和最小值,然后利用不等式恒成立的条件进行求参数a的取值范围..
| 1 |
| 2 |
| 1 |
| 2 |
(2)求出函数f(x)在区间[1,a]上的最大值和最小值,然后利用不等式恒成立的条件进行求参数a的取值范围..
解答:
解:(1)由已知x>0,f′(x)=x+
由于曲线y=f(x)在(2,f(2))处切线的斜率为
,
所以f′(2)=
,即2+
=
,解得a=-3
所以f(x)=
x2-3lnx,f′(x)=x-
令f′(x)=0,则x=
或x=-
(舍)
当0<x<
时,f′(x)<0,函数f(x)单调递减;
当x>
时,f′(x)>0,函数f(x)单调递增.
故x=
是f(x)的极大值点,且f(x)的极大值为f(
)=
(1-ln3);
(2)证明:由于F(x)=f(x)-g(x)=
x2+alnx-(a+1)x(x>0),
则F′(x)=x+
-(a+1)=
=
,
由于x>0,a∈(1,e],
故当0<x<1或x>a时,F′(x)>0,
当1<x<a时,F′(x)<0,
故函数F(x)在[1,a]上为单调递减函数.
所以Fmin=F(a)=
a2+alna-(a+1)a=-
a2+alna-a,
Fmax=F(1)=-a-
故对?x1,x2∈[1,a],|F(x1)-F(x2)|max=F(1)-F(a)=
a2-alna-
,
又因为a∈(1,e],
所以
a2-alna-
≤
e2-e-
<1,
所以当x1,x2∈[1,a]时,|F(x1)-F(x2)|<1恒成立.
| •a |
| x |
由于曲线y=f(x)在(2,f(2))处切线的斜率为
| 1 |
| 2 |
所以f′(2)=
| 1 |
| 2 |
| a |
| 2 |
| 1 |
| 2 |
所以f(x)=
| 1 |
| 2 |
| 3 |
| x |
令f′(x)=0,则x=
| 3 |
| 3 |
当0<x<
| 3 |
当x>
| 3 |
故x=
| 3 |
| 3 |
| 3 |
| 2 |
(2)证明:由于F(x)=f(x)-g(x)=
| 1 |
| 2 |
则F′(x)=x+
| •a |
| x |
| x2-(a+1)x+a |
| x |
| (x-1)(x-a) |
| x |
由于x>0,a∈(1,e],
故当0<x<1或x>a时,F′(x)>0,
当1<x<a时,F′(x)<0,
故函数F(x)在[1,a]上为单调递减函数.
所以Fmin=F(a)=
| 1 |
| 2 |
| 1 |
| 2 |
Fmax=F(1)=-a-
| 1 |
| 2 |
故对?x1,x2∈[1,a],|F(x1)-F(x2)|max=F(1)-F(a)=
| 1 |
| 2 |
| 1 |
| 2 |
又因为a∈(1,e],
所以
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
所以当x1,x2∈[1,a]时,|F(x1)-F(x2)|<1恒成立.
点评:本题考查导数在研究函数中的应用:要求学生会求曲线上过某点的切线方程的斜率,会利用导数研究函数的极值.研究函数的单调性以及求函数的最大值和最小值.要使不等式恒成立,只要1大于等于最大值与最小值之差即可.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
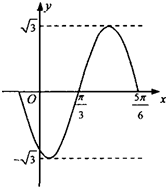 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示,为了得到g(x)=
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的部分图象如图所示,为了得到g(x)=| 3 |
A、向左平移
| ||
B、向左平移
| ||
C、向右平移
| ||
D、向右平移
|