题目内容
1.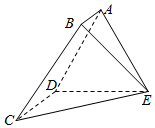 如图,在空间多面体ABCDE中,四边形ABCD为直角梯形,AB∥DC,AD⊥CD,△ADE是正三角形,CD=DE=2AB=2a,CE=$\sqrt{2}$CD.
如图,在空间多面体ABCDE中,四边形ABCD为直角梯形,AB∥DC,AD⊥CD,△ADE是正三角形,CD=DE=2AB=2a,CE=$\sqrt{2}$CD.(1)求证:平面CDE⊥平面ADE;
(2)求多面体ABCDE的体积.
分析 (1)利用勾股定理的逆定理可得CD⊥DE,结合AD⊥CD得出CD⊥平面ADE,从而平面CDE⊥平面ADE;
(2)作EG⊥AD,则可证明EG⊥平面ABCD,于是多面体体积等于四棱锥E-ABCD的体积.
解答  证明:(1)∵CD=DE,CE=$\sqrt{2}$CD,
证明:(1)∵CD=DE,CE=$\sqrt{2}$CD,
∴CD2+DE2=CE2,
∴CD⊥DE
又CD⊥AD,AD?平面ADE,DE?平面ADE,AD∩DE=D,
∴CD⊥平面ADE,又CD?平面CDE,
∴平面CDE⊥平面ADE.
(2)过E作EG⊥AD,垂足为G,
∵CD⊥平面ADE,GE?平面ADE,
∴CD⊥GE,
又GE⊥AD,AD?平面ABCD,CD?平面ABCD,AD∩CD=D,
∴GE⊥平面ABCD.
∵△ADE是等边三角形,DE=2a,
∴GE=$\sqrt{3}a$.
∵S梯形ABCD=$\frac{1}{2}$(AB+CD)•AD=$\frac{1}{2}×$(a+2a)•2a=3a2.
∴多面体ABCDE的体积V=VE-ABCD=$\frac{1}{3}{S}_{梯形ABCD}•EG$=$\frac{1}{3}×3{a}^{2}×\sqrt{3}a$=$\sqrt{3}$a3.
点评 本题考查了面面垂直的判定,棱锥的体积计算,属于中档题.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
11.已知抛物线C:y2=6x的焦点为F,准线为l,点P在C上,点Q在l上,若$\overrightarrow{PF}$=$\overrightarrow{FQ}$,则直线PQ的斜率为( )
| A. | ±1 | B. | ±$\sqrt{2}$ | C. | ±$\sqrt{3}$ | D. | ±2 |
10.已知某工程在很大程度上受当地年降水量的影响,施工期间的年降水量X(单位:mm)对工期延误天数Y的影响及相应的概率P如表所示:
在降水量X至少是100的条件下,工期延误不超过15天的概率为( )
| 降水量X | X<100 | 100≤X<200 | 200≤X<300 | X≥300 |
| 工期延误天数Y | 0 | 5 | 15 | 30 |
| 概率P | 0.4 | 0.2 | 0.1 | 0.3 |
| A. | 0.1 | B. | 0.3 | C. | 0.42 | D. | 0.5 |
10.己知集合A={x|2x≥1},B={x|x2-3x+2≥0},则A∩B=( )
| A. | {x|x≤0} | B. | {x|1≤x≤2} | C. | {x|0≤x≤1或x≥2} | D. | {x|0≤x<或x≥2} |
 如图,已知正四棱柱ABCD-A1B1C1D1的体积为36,点E,F分别为棱B1B,C1C上的点(异于端点),且EF∥BC,则四棱锥A1-AEFD的体积为12.
如图,已知正四棱柱ABCD-A1B1C1D1的体积为36,点E,F分别为棱B1B,C1C上的点(异于端点),且EF∥BC,则四棱锥A1-AEFD的体积为12.