题目内容
6.一个球与正三棱柱的三个侧面和两个底面都相切,已知这个球的体积为36π,那么该三棱柱的体积是162$\sqrt{3}$.分析 根据球的体积得出球的半径,由球与棱柱相切可知棱柱的高为球的直径,棱柱底面三角形的内切圆为球的大圆,从而计算出棱柱的底面边长和高.
解答 解:设球的半径为r,则$\frac{4π{r}^{3}}{3}$=36π,解得r=3.
∵球与正三棱柱的三个侧面相切,
∴球的大圆为棱柱底面等边三角形的内切圆,
∴棱柱底面正三角形的边长为2$\sqrt{3}r$=6$\sqrt{3}$.
∵球与棱柱的两底面相切,
∴棱柱的高为2r=6.
∴三棱柱的体积V=$\frac{\sqrt{3}}{4}×(6\sqrt{3})^{2}×6$=162$\sqrt{3}$.
故答案为162$\sqrt{3}$.
点评 本题考查了棱柱与内切球的关系,找出球的半径与棱柱的关系是解题关键.

练习册系列答案
相关题目
16.平面上有两定点A、B和动点P,|PA|=2|PB|,则动点P的轨迹为( )
| A. | 椭圆 | B. | 圆 | C. | 双曲线 | D. | 抛物线 |
18.执行如图所示的程序框图,如果输入的t=0.02,则输出的n=( )


| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
15.已知函数f(x)=2sinxsin(x+3φ)是奇函数,其中φ∈(0,$\frac{π}{2}$),则函数g(x)=cos(2x-φ)的图象( )
| A. | 关于点($\frac{π}{12}$,0)对称 | |
| B. | 可由函数f(x)的图象向右平移$\frac{π}{3}$个单位得到 | |
| C. | 可由函数f(x)的图象向左平移$\frac{π}{6}$个单位得到 | |
| D. | 可由函数f(x)的图象向左平移$\frac{π}{3}$个单位得到 |
15.已知tanα=2,则sin2α=( )
| A. | $\frac{4}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{2}{5}$ | D. | 4 |
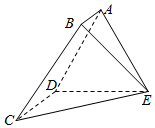 如图,在空间多面体ABCDE中,四边形ABCD为直角梯形,AB∥DC,AD⊥CD,△ADE是正三角形,CD=DE=2AB=2a,CE=$\sqrt{2}$CD.
如图,在空间多面体ABCDE中,四边形ABCD为直角梯形,AB∥DC,AD⊥CD,△ADE是正三角形,CD=DE=2AB=2a,CE=$\sqrt{2}$CD.