题目内容
11．已知抛物线C：y2=6x的焦点为F，准线为l，点P在C上，点Q在l上，若$\overrightarrow{PF}$=$\overrightarrow{FQ}$，则直线PQ的斜率为（ ）| A． | ±1 | B． | ±$\sqrt{2}$ | C． | ±$\sqrt{3}$ | D． | ±2 |
分析 利用抛物线的定义，结合 $\overrightarrow{PF}$=$\overrightarrow{FQ}$，求出P的坐标，即可求解直线的斜率．
解答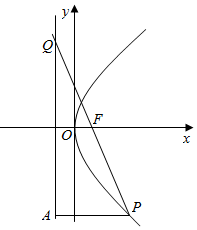 
解：抛物线Γ：y2=6x的焦点F（$\frac{3}{2}$，0），$\overrightarrow{PF}$=$\overrightarrow{FQ}$，
|QF|=|PF|=|PA|，
∵2p=6，P（$\frac{9}{2}$，±3$\sqrt{3}$）
∴直线PQ的斜率就是直线PF的斜率kPF=±$\frac{3\sqrt{3}-0}{\frac{9}{2}-\frac{3}{2}}$=$±\sqrt{3}$，
故选：C．
点评 本题考查抛物线的简单性质，考查直线与抛物线的位置关系，属于基础题．
练习册系列答案
相关题目
11．已知A，B，O三点不共线，若|$\overrightarrow{AB}$|=|$\overrightarrow{OA}$+$\overrightarrow{OB}$|，则向量$\overrightarrow{OA}$与$\overrightarrow{OB}$的夹角为（ ）
| A． | 锐角 | B． | 直角 | C． | 钝角 | D． | 锐角或钝角 |
6．两枚均匀的骰子一起投掷，记事件A={至少有一枚骰子6点向上}，B={两枚骰子都是6点向上}，则P（B|A）=（ ）
| A． | $\frac{1}{6}$ | B． | $\frac{1}{36}$ | C． | $\frac{1}{12}$ | D． | $\frac{1}{11}$ |
16．平面上有两定点A、B和动点P，|PA|=2|PB|，则动点P的轨迹为（ ）
| A． | 椭圆 | B． | 圆 | C． | 双曲线 | D． | 抛物线 |
如图给出一个“直角三角形数阵”，满足每一列成等差数列，从第三行起每一行的数成等比数列，且每一行的公比相等，记第i行、第j列的数为ai，j（i≥j，I，j∈N*），则a5，j=5（$\frac{1}{2}$）j+1，，ai，5=$\frac{i}{64}$．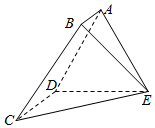
如图，在空间多面体ABCDE中，四边形ABCD为直角梯形，AB∥DC，AD⊥CD，△ADE是正三角形，CD=DE=2AB=2a，CE=$\sqrt{2}$CD．