题目内容

函数y=cosωx（ω＞0）在区间[0，1）上至少出现2次最大值，至多出现3次最大值，则ω的取值范围是（　　）
A、2π≤ω≤4π
B、2π＜ω≤4π
C、2π＜ω≤6π
D、2π＜ω＜6π
考点：余弦函数的定义域和值域
专题：三角函数的图像与性质
分析：首先，函数y=cosωx（ω＞0）的周期为T=
2π
ω
，然后，根据条件，得到
2
3
＜T≤1，然后，求解ω范围．
解答： 解：∵函数y=cosωx（ω＞0）的周期为T=
2π
ω
，
且在区间[0，1）上至少出现2次最大值，至多出现3次最大值，
∴
2
3
＜T≤1，
即
2
3
＜
2π
ω
≤1，
解得2π＜ω≤6π，
故选：C．
点评：本题重点考查了三角函数的图象与性质等知识，属于中档题．
练习册系列答案
相关题目
圆（x-1）2+（y-1）2=1的圆心坐标和半径是（　　）
A、（0，1），1
B、（1，1），1
C、（-1，-1），1
D、（1，0），1
如图放置的几何体的俯视图为（　　）
A、
B、
C、
D、
若关于x的不等式a≤
3
4
x2-3x+4≤b的解集恰好是[a，b]，则b-a的值为（　　）
A、1B、2C、3D、4
下列各组函数中，表示同一函数的是（　　）
A、y=x与y=
x2
B、y=
x-1
与y=
x-1
x-1
 
C、y=4lgx与y=2lgx2
D、y=-2+lgx与y=lg
x
100
在△ABC中，AB=1，BC=2，B=60°，M为AC中点，则
AB
•
AM
的值为（　　）
A、0
B、1
C、
3
D、2
函数f（x）=2sin（
2
3
x+
15π
2
）是（　　）
A、周期为3π的偶函数
B、周期为3π的奇函数
C、周期为
4π
3
的偶函数
D、周期为
4π
3
的奇函数
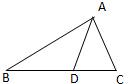如图，已知
AB
=
a
，
AC
=
b
，
BD
=3
DC
，用
a
、
b
表示
AD
，则
AD
等于（　　）
A、
a
+
3
4
b
B、
3
4
a
+
1
4
b
C、
1
4
a
+
1
4
b
D、
1
4
a
+
3
4
b
函数y=
2cosx-1
的定义域是（　　）
A、[2kπ-
π
3
，2kπ+
π
3
]（k∈Z）
B、[2kπ-
π
6
，2kπ+
π
6
]（k∈Z）
C、[2kπ+
π
3
，2kπ+
2π
3
]（k∈Z）
D、[2kπ-
2π
3
，2kπ+
2π
3
]（k∈Z）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网