题目内容
f（x）=x3+bx2+cx+d的导函数f′（x）的图象关于直线x=2对称，则b的值为（ ）
| A、-3 | B、3 | C、1 | D、-6 |
考点：导数的运算
专题：导数的综合应用
分析：求出函数的导数，根据导函数f′（x）的图象的对称性即可得到结论．
解答：
解：函数的导数为f′（x）=3x2+2bx+c，
∵导函数f′（x）的图象关于直线x=2对称，
∴-
=-
=2，解得b=-6，
故选：D
∵导函数f′（x）的图象关于直线x=2对称，
∴-
| 2b |
| 2×3 |
| b |
| 3 |
故选：D
点评：本题主要考查导数的运算，利用二次函数的对称性是解决本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
圆（x-1）2+（y-1）2=1的圆心坐标和半径是（ ）
| A、（0，1），1 |
| B、（1，1），1 |
| C、（-1，-1），1 |
| D、（1，0），1 |
关于平面向量
，
，
有下列三个命题：
①若
•
=
•
，则
=
②若
=（1，k）
=（-2，6），
⊥
则k=
③非零向量
和
满足|
|=|
|=|
-
|，则
与
+
的夹角为60°，
其中真命题的序号为（ ）
| a |
| b |
| c |
①若
| a |
| b |
| a |
| c |
| b |
| c |
②若
| a |
| b |
| a |
| b |
| 1 |
| 3 |
③非零向量
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| a |
| b |
其中真命题的序号为（ ）
| A、①② | B、② | C、②③ | D、①②③ |
由“正三角形的内切圆切于三边的中点”，可类比猜想出正四面体的内切球切于四个侧面三角形 （ ）
| A、内任一点 | B、某高线上的点 |
| C、中心 | D、外的某点 |
下列四组函数中表示同一函数的是（ ）
A、f（x）=x，g（x）=（
| |||||||
| B、f（x）=x2，g（x）=（x+1）2 | |||||||
C、f（x）=
| |||||||
D、f（x）=0，g（x）=
|
如图放置的几何体的俯视图为（ ）A、 |
B、 |
C、 |
D、 |
若关于x的不等式a≤
x2-3x+4≤b的解集恰好是[a，b]，则b-a的值为（ ）
| 3 |
| 4 |
| A、1 | B、2 | C、3 | D、4 |
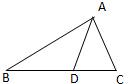如图，已知| AB |
| a |
| AC |
| b |
| BD |
| DC |
| a |
| b |
| AD |
| AD |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|