题目内容
11.已知定义在R上的奇函数f(x)满足f(1)=e(e为自然对数的底数),且当x≥0时,有(x-1)f(x)<xf'(x),则不等式xf(x)-e|x|>0的解集是( )| A. | (-∞,-1)∪(1,+∞) | B. | (-1,0)∪(0,1) | C. | (-1,1) | D. | (-1,0)∪(1,+∞) |
分析 构造函数g(x)=$\frac{xf(x)}{{e}^{|x|}}$,确定函数的单调性与奇偶性,即可解不等式.
解答 解:构造函数g(x)=$\frac{xf(x)}{{e}^{|x|}}$,则当x≥0时,g′(x)=$\frac{xf′(x)-(x-1)f(x)}{{e}^{x}}$>0,函数单调递增,
∵f(x)是奇函数,∴g(x)是偶函数,
xf(x)-e|x|>0等价于g(x)>g(1),
∴|x|>1,
∴x<-1或x>1,
故选A.
点评 本题考查函数的单调性与奇偶性,考查学生解不等式的能力,正确构造函数是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.已知向量$\overrightarrow{a}$=(5,k),$\overrightarrow{b}$=(2,-2),则使|$\overrightarrow{a}-\overrightarrow{b}$|≤5成立的充分不必要条件是( )
| A. | -6≤k≤2 | B. | -6≤k≤-2 | C. | -2≤k≤6 | D. | 2≤k≤6 |
6.“a>b”是“lna>lnb”的( )
| A. | 充要条件 | B. | 充分不必要条件 | ||
| C. | 必要不充分条件 | D. | 既不充分也不必要条件 |
3.若复数z满足(z-3)(1-3i)=10(i为虚数单位),则z的模为( )
| A. | $\sqrt{5}$ | B. | 5 | C. | $2\sqrt{6}$ | D. | 25 |
20.在长为16cm的线段MN上任取一点P,以MP,NP为邻边作一矩形,则该矩形的面积大于60cm2的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{3}{4}$ |
1.已知集合A={x|x2-x-6≥0},B={x|-3≤x≤3},则A∩B等于( )
| A. | [-3,-2] | B. | [2,3] | C. | [-3,-2]∪{3} | D. | [2,3]∪{-3} |
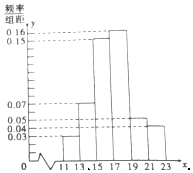 一企业从某生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到的频率分布直方图如图.
一企业从某生产线上随机抽取100件产品,测量这些产品的某项技术指标值x,得到的频率分布直方图如图.