题目内容
如图所示,在长方形ABCD中,AB=2,BC=1,E为DC的中点,F为线段EC(端点除外)上一动点.现将△AFD沿AF折起,使平面ABD⊥平面ABCF.在平面ABD内过点D作DK⊥AB,K为垂足.设AK=t,则t的取值范围是 .


 解析:如图所示,过D作DG⊥AF,垂足为G,连接GK,
解析:如图所示,过D作DG⊥AF,垂足为G,连接GK,
∵平面ABD⊥平面ABCF,
DK⊥AB,
∴DK⊥平面ABCF,
∴DK⊥AF.
而DG∩DK=D,
∴AF⊥平面DKG,
∴AF⊥GK.
容易得到,当F接近E点时K接近AB的中点,
当F接近C点时,K接近AB的四等分点,
∴t的取值范围是 .
.

练习册系列答案
相关题目

 A1B1C1D1的底面ABCD的中心,则下列直线中与B1O垂直的是( )
A1B1C1D1的底面ABCD的中心,则下列直线中与B1O垂直的是( )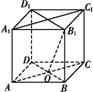
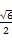 倍,则侧面与底面所成锐二面角等于 .
倍,则侧面与底面所成锐二面角等于 . 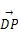 ,
,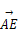 >=
>=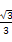 ,若以DA,DC,DP所在直线分别为x,y,z轴建立空间直角坐标系,则点E的坐标为( )
,若以DA,DC,DP所在直线分别为x,y,z轴建立空间直角坐标系,则点E的坐标为( )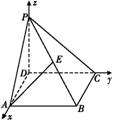
 )
) ) (D)(1,1,2)
) (D)(1,1,2) A′B′C′D′.设M是底面ABCD的中心,N是侧面BCC′B′的对角线BC′上的点,且BN∶
A′B′C′D′.设M是底面ABCD的中心,N是侧面BCC′B′的对角线BC′上的点,且BN∶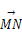 =α
=α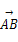 +β
+β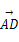 +γ
+γ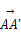 ,试求α,β,γ之值.
,试求α,β,γ之值.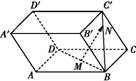
 BD
BD