题目内容
15.如果一个函数f(x)在定义域D中满足:(1)任意x1,x2∈D,f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{f({x}_{1})+f({x}_{2})}{2}$;(2)存在x1,x2∈D,且x1≠x2,使得f(x1)=f(x2),则f(x)可以是( )| A. | f(x)=x2+2x | B. | f(x)=cosx | C. | f(x)=2x-1 | D. | f(x)=$\frac{1}{2}$(ex-e-x) |
分析 根据条件分别进行验证,依次进行判断即可.
解答 解:A.∵f($\frac{{x}_{1}+{x}_{2}}{2}$)-$\frac{f({x}_{1})+f({x}_{2})}{2}$=($\frac{{x}_{1}+{x}_{2}}{2}$)2+2×($\frac{{x}_{1}+{x}_{2}}{2}$)-$\frac{1}{2}$x12-x1-$\frac{1}{2}$x22-x2=-$\frac{({x}_{1}-{x}_{2})^{2}}{4}$<0恒成立,
即f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{f({x}_{1})+f({x}_{2})}{2}$;成立,满足条件.
B.f(x)=cosx的图象不满足条件.比如当x1=0,x2=$\frac{π}{2}$时,f($\frac{{x}_{1}+{x}_{2}}{2}$)=f($\frac{π}{4}$)=cos$\frac{π}{4}$=$\frac{\sqrt{2}}{2}$,
$\frac{f({x}_{1})+f({x}_{2})}{2}$=$\frac{1}{2}$(0+1)=$\frac{1}{2}$,不满足条件f($\frac{{x}_{1}+{x}_{2}}{2}$)≤$\frac{f({x}_{1})+f({x}_{2})}{2}$.
C.f(x)=2x-1为单调函数,不满足条件.
D.f(x)=$\frac{1}{2}$(ex-e-x)为单调函数,不满足条件.
故选:A
点评 本题主要考查抽象函数的应用,根据定义转化为进行判断或者使用排除法是解决本题的关键.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目
5.函数f(x)=Asin(ωx+φ)的部分图象如图所示,则函数的解析式可以是( )
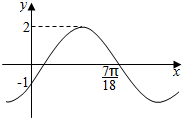

| A. | f(x)=2cos(3x+$\frac{2π}{3}$) | B. | f(x)=2sin($\frac{15}{7}x-\frac{5π}{6}$) | ||
| C. | f(x)=2sin(3x-$\frac{π}{6}$) | D. | f(x)=2sin(3x-$\frac{π}{6}$)或f(x)=2sin($\frac{15}{7}x-\frac{5π}{6}$) |
6.某学校共有3125名学生,一次活动中全体学生被排成一个n排的等腰梯形阵,且这n排学生数按每排都比前一排
多一人的规律排列,则当n取到最大值时,排在这等腰梯形阵最外面的一周的学生总人数是( )
多一人的规律排列,则当n取到最大值时,排在这等腰梯形阵最外面的一周的学生总人数是( )
| A. | 296 | B. | 221 | C. | 225 | D. | 641 |
7.已知函数f(x)=2sin2(ωx+$\frac{π}{6}$)(ω>0)在区间[$\frac{π}{6}$,$\frac{2π}{3}$]内单调递增,则ω的最大值是( )
| A. | $\frac{3}{4}$ | B. | $\frac{3}{5}$ | C. | $\frac{1}{2}$ | D. | $\frac{1}{4}$ |