题目内容
11.已知函数f(x)的定义域为(2+3a,2-a),且f(x+1)为奇函数,则a的值为-1.分析 根据f(x)的定义域便可求出f(x+1)的定义域为(1+3a,1-a),而由f(x+1)为奇函数便知其定义域关于原点对称,从而便可求出a的值.
解答 解:f(x)的定义域为(2+3a,2-a);
∴f(x+1)中的x满足2+3a<x+1<2-a;
∴1+3a<x<1-a;
∵f(x+1)为奇函数;
∴f(x+1)的定义域关于原点对称;
∴1+3a+1-a=0;
∴a=-1.
故答案为:-1.
点评 考查函数定义域的概念及求法,由函数f(x)求函数f[g(x)]定义域的方法,以及奇函数的定义,奇函数定义域的对称性.

练习册系列答案
相关题目
1.若[x]表示不超过x的最大整数,执行如图所示的程序框图,则输出S的值为( )


| A. | 3 | B. | 5 | C. | 7 | D. | 10 |
19.在k进制中,十进制数103记为87,则k等于( )
| A. | 6 | B. | 12 | C. | 14 | D. | 16 |
3.在直二面角α-l-β中,线段AB的端点A,B分别在α,β内,且AB与α,β所成的角均为30°,则AB与l所成的角为( )
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
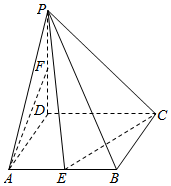 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E,F分别为AB和PD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠DAB=60°,PD⊥平面ABCD,PD=AD=2,点E,F分别为AB和PD的中点.