题目内容
1.已知集合A={(x,y)|-1≤x≤2且0≤y≤4},集合B={(x,y)|0≤y≤x2},在A中任取一点P,则P∈B的概率为( )| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
分析 分别求出集合A,B对应的去面积,利用几何概型的概率公式解答
解答  解:由题意,集合A,B对应的区域如图集合A是图中矩形部分,集合B是图中阴影部分
解:由题意,集合A,B对应的区域如图集合A是图中矩形部分,集合B是图中阴影部分
它们的面积分别为3×4=12,阴影部分的面积为${∫}_{-1}^{2}{x}^{2}dx$=$\frac{1}{3}{x}^{3}{|}_{-1}^{2}$=3,
所以在集合A中任取一点P,则P∈B的概率是$\frac{3}{12}=\frac{1}{4}$;
故选:D.
点评 本题主要考查几何概型的概率公式的计算,根据条件求出相应的面积是解决本题的关键.

练习册系列答案
相关题目
11.若a=($\frac{1}{2}$)${\;}^{\frac{1}{3}}$,b=$lo{g_{\frac{1}{3}}}$2,c=lo${g_{\frac{1}{2}}}$3,则a,b,c三者的大小关系是( )
| A. | b>c>a | B. | c>a>b | C. | a>b>c | D. | a>c>b |
12.已知全集U=R,集合P={x|x2-2x≤0},Q={y|y=x2-2x},则P∩Q为( )
| A. | [-1,2] | B. | [0,2] | C. | [0,+∞) | D. | [-1,+∞) |
9.若复数z的共轭复数为$\overline{z}$,且满足:$\frac{\overline{z}}{1+i}$=1-2i,其中i为虚数单位,则复数z的模为( )
| A. | 1 | B. | 3 | C. | $\sqrt{10}$ | D. | 4 |
6.设集合A={x|x2-2x≥0},B={x|-1<x<2},则A∩B=( )
| A. | {x|0≤x≤2} | B. | {x|0<x<2} | C. | {x|-1≤x<0} | D. | {x|-1<x≤0} |
10.已知条件p:x≥1,条件q:$\frac{1}{x}$<1,则¬p是q的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
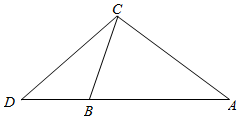 如图,在锐角三角形ABC中,∠A=$\frac{π}{4}$,AC=$\sqrt{3}$,BC=$\sqrt{2}$,BD=$\frac{3\sqrt{2}}{5}$;
如图,在锐角三角形ABC中,∠A=$\frac{π}{4}$,AC=$\sqrt{3}$,BC=$\sqrt{2}$,BD=$\frac{3\sqrt{2}}{5}$;