题目内容
16.直线m经过抛物线C:y2=4x的焦点F,与C交于A,B两点,且|AF|+|BF|=10,则线段AB的中点D到y轴的距离为4.分析 根据抛物线的方程求出准线方程,利用抛物线的定义抛物线上的点到焦点的距离等于到准线的距离,列出方程求出A,B的中点横坐标的和,求出线段AB的中点到y轴的距离.
解答 解:由已知点F(1,0),抛物线C的准线l:x=-1,
设A(x1,y1),B(x2,y2)
∴|AF|+|BF|=x1+1+x2+1=10,
∴x1+x2=8
∴线段AB的中点横坐标为4
∴线段AB的中点到y轴的距离为4.
故答案为4.
点评 本题考查解决抛物线上的点到焦点的距离问题,解题的关键是利用抛物线的定义将到焦点的距离转化为到准线的距离.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知函数f(x)=Asin(2x+φ)-$\frac{1}{2}$(A>0,0<φ<$\frac{π}{2}$)的图象在y轴上的截距为1,且关于直线x=$\frac{π}{12}$对称,若对于任意的x∈[0,$\frac{π}{2}$],都有m2-3m≤f(x),则实数m的取值范围为( )
| A. | [1,$\frac{3}{2}$] | B. | [1,2] | C. | [$\frac{3}{2}$,2] | D. | [$\frac{3-\sqrt{3}}{2}$,$\frac{3+\sqrt{3}}{2}$] |
11.在Rt△ABC中,∠B=60°过直角顶点A在∠BAC内随机作射线AD,交斜边BC于点D,则BD>BA的概率为( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{3}}}{4}$ |
1.已知$λ=3\int_0^1{{x^2}dx}$,在矩形ABCD中,AB=2,AD=1,点P为矩形ABCD内一点,则使得$\overrightarrow{AP}•\overrightarrow{AC}≥λ$的概率为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{4}$ | C. | $\frac{3}{4}$ | D. | $\frac{7}{8}$ |
8.在复平面内,复数$z=\frac{-1+i}{2-i}$(i为虚数单位)的共轭复数对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.已知函数f ( x)=2ax-a+3,若?x0∈(-1,1),f ( x0 )=0,则实数 a 的取值范围是( )
| A. | (-∞,-3)∪(1,+∞) | B. | (-∞,-3) | C. | (-3,1) | D. | (1,+∞) |
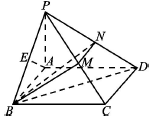 如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥BC.
如图,四棱锥P-ABCD,底面ABCD为矩形,AB=PA=$\sqrt{3}$,AD=2,PB=$\sqrt{6}$,E为PB中点,且AE⊥BC.