题目内容
1.函数f(x)=|x2-a|在区间[-1,1]上的最大值是a,那么实数a的取值范围是( )| A. | [0,+∞) | B. | [$\frac{1}{2}$,1] | C. | [$\frac{1}{2}$,+∞) | D. | [1,+∞) |
分析 对a讨论,分a≤0,a>0,可得a>0成立,由|x2-a|=a,可得x=0或±$\sqrt{2a}$,由$\sqrt{2a}$≥1,即可得到所求范围.
解答 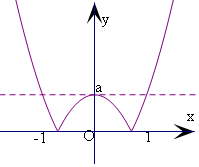 解:若a≤0,则f(x)=x2-a,
解:若a≤0,则f(x)=x2-a,
f(x)在[-1,1]的最大值为1-a,
即有1-a=a,可得a=$\frac{1}{2}$,不成立;
则a>0,由|x2-a|=a,可得x=0或±$\sqrt{2a}$,
由图象结合在区间[-1,1]上的最大值是a,
可得$\sqrt{2a}$≥1,解得a≥$\frac{1}{2}$.
故选:C.
点评 本题考查函数的最值的判断,考查分类讨论思想方法,数形结合思想,以及运算能力,属于中档题.

练习册系列答案
相关题目
16.已知锐角三角形三边长分别为1,3,a,则a的取值范围是( )
| A. | 8<a<10 | B. | 2$\sqrt{2}<a<\sqrt{10}$ | C. | $2\sqrt{2}<a<10$ | D. | $\sqrt{10}<a<8$ |
11.若a=log20.5,b=20.5,c=0.52,则a,b,c三个数的大小关系是( )
| A. | a<b<c | B. | b<c<a | C. | a<c<b | D. | c<a<b |
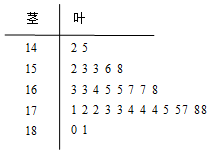 从某校的高一学生中采用系统抽样法选出30人测量其身高,数据的茎叶图如图(单位:cm):若高一年级共有600人,据上图估算身高在1.70m以上的大约有300人.
从某校的高一学生中采用系统抽样法选出30人测量其身高,数据的茎叶图如图(单位:cm):若高一年级共有600人,据上图估算身高在1.70m以上的大约有300人.