题目内容
16.已知函数f(x)=x3+3ax2-bx,曲线y=f(x)在点(1,f(1))处的切线方程为y=-12x+1(1)试确定a,b的值;
(2)求f(x)的单调区间.
分析 (1)根据导数的几何意义求出函数在x=1处的导数,从而得到切线的斜率,建立等式关系,再根据切点在函数图象建立等式关系,解方程组即可求出a和b,从而得到函数f(x)的解析式;
(2)由(1)得f′(x),令f′(x)>0和令f′(x)<0,即可求出函数f(x)的单调区间.
解答 解:(1)函数f(x)=x3+3ax2-bx,可得f′(x)=3x2+6ax-b,f′(1)=3+6a-b=-12.①
又x=1,y=-11在f(x)的图象上,
∴1+3a-b=-11.②
由①②得a=-1,b=9,
(2)f(x)=x3-x2-9x.
f′(x)=3x2-6x-9,令f′(x)<0,得:3x2-6x-9<0,
可得-1<x<3,
∴函数f(x)的单调减区间为(-1,3),单调增区间为:(-∞,-1),(3,+∞).
点评 本题主要考查了利用导数研究曲线上某点切线方程,以及导函数的正负与原函数的单调性之间的关系等基础题知识,考查运算求解能力,考查数形结合思想,属于中档题.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
7.已知点O为坐标原点,点An(n,αn)(n∈N*)为函数f(x)=$\frac{1}{x+1}$的图象上的任意一点,向量$\overrightarrow{i}$=(0,1).θn是向量$\overrightarrow{O{A}_{n}}$与$\overrightarrow{i}$的夹角,则数列|$\frac{cos{θ}_{n}}{sin{θ}_{n}}$|的前2015项的和为( )
| A. | 2 | B. | $\frac{2014}{2015}$ | C. | $\frac{2015}{2016}$ | D. | 1 |
8.已知a,b∈R,则“a+b>2”是“a>1或b>1”( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不必要也不充分条件充要条件 |
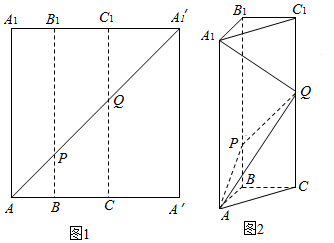
 如图,在多面体ABCDE中,BD⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.
如图,在多面体ABCDE中,BD⊥平面ABC,AE∥DB,且△ABC是边长为2的等边三角形,2AE=BD=2.