题目内容
17.(Ⅰ)求值:$\frac{{tan150°cos{{210}°}sin({-60°})}}{{sin(-30°)cos{{120}°}}}$;(Ⅱ)化简:$\frac{sin(-α)cos(π+α)tan(2π+α)}{cos(2π+α)sin(π-α)tan(-α)}$.
分析 (Ⅰ)利用诱导公式以及特殊角的三角函数化简求解即可;
(Ⅱ)利用诱导公式转化求解即可.
解答 解:(Ⅰ)原式=$\frac{{-tan3{0^0}(-cos3{0^0})(-sin6{0^0})}}{{-sin{{30}^0}(-cos{{60}^0})}}$=$-tan{60^0}=-\sqrt{3}$.…(5分)
(Ⅱ)原式=$\frac{-sinα(-cosα)tanα}{cosαsinα(-tanα)}=\frac{sinαcosαtanα}{-cosαsinαtanα}=-1$.…(10分)
点评 本题考查诱导公式的应用,三角函数化简求值,考查计算能力.

练习册系列答案
相关题目
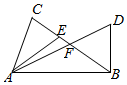 如图,F为线段BC的中点,CE=2EF,$DF=\frac{3}{5}AF$,设$\overrightarrow{AC}=a$,$\overrightarrow{AB}=b$,试用a,b表示$\overrightarrow{AE}$,$\overrightarrow{AD}$,$\overrightarrow{BD}$.
如图,F为线段BC的中点,CE=2EF,$DF=\frac{3}{5}AF$,设$\overrightarrow{AC}=a$,$\overrightarrow{AB}=b$,试用a,b表示$\overrightarrow{AE}$,$\overrightarrow{AD}$,$\overrightarrow{BD}$.