题目内容
20.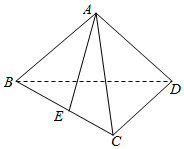 如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.
如图,在三棱锥A-BCD中,CD⊥BD,AB=AD,E为BC的中点.(I)求证:AE⊥BD;
(Ⅱ)设平面ABD⊥平面BCD,AD=CD=2,BC=4,求二面角B-AC-D的正弦值.
分析 (1)根据线面垂直的性质定理进行证明即可.
(2)建立空间直角坐标系,求平面的法向量,利用向量法进行求解.
解答 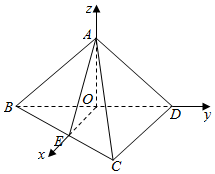 证明:(I)∵AB=AD,E为BC的中点,
证明:(I)∵AB=AD,E为BC的中点,
∴取BD的中点0,
连接AO,OE,
则OA⊥BD,OE是△BCD的中位线,
∴OE∥CD,
∵CD⊥BD,∴OE⊥BD,
∵BD∩OA=O,
∴AE⊥BD;
(Ⅱ)设平面ABD⊥平面BCD,
∵OA⊥BD,∴OA⊥面BCD,
建立以O为坐标原点,OE,OD,OA分别为x,y,z轴的空间直角坐标系如图:
∵AD=CD=2,BC=4,
∴OA=1,OB=OD=$\sqrt{3}$,
则B(0,-$\sqrt{3}$,0),D(0,$\sqrt{3}$,0),A(0,0,1),C(2,$\sqrt{3}$,0),
则$\overrightarrow{AB}$=(0,-$\sqrt{3}$,-1),$\overrightarrow{AC}$=(2,$\sqrt{3}$,-1),$\overrightarrow{AD}$=(0,$\sqrt{3}$,-1),
设平面ABC的一个法向量为$\overrightarrow{m}$=(x,y,z),
则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{AB}=-\sqrt{3}y-z=0}\\{\overrightarrow{m}•\overrightarrow{AC}=2x+\sqrt{3}y-z=0}\end{array}\right.$,
令y=-$\sqrt{3}$,则z=3,x=3,即$\overrightarrow{m}$=(3,-$\sqrt{3}$,3),
同理可求平面ACD的一个法向量为$\overrightarrow{n}$=(0,$\sqrt{3}$,3),
|cos<$\overrightarrow{m}$,$\overrightarrow{n}$>|=|$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}$|=$\frac{\sqrt{7}}{7}$,
则sin<$\overrightarrow{m}$,$\overrightarrow{n}$>=$\sqrt{1-(\frac{\sqrt{7}}{7})^{2}}$=$\frac{\sqrt{42}}{7}$
则二面角B-AC-D的正弦值$\frac{\sqrt{42}}{7}$.
点评 本小题主要考直线垂直的判断和二面角的求解,考查用空间向量解决立体几何问题的方法,考查空间想象能力、运算能力和推理论证能力,综合性较强,运算量较大.

| A. | 36种 | B. | 30种 | C. | 24种 | D. | 20种 |
| A. | $-\frac{1}{5}+\frac{2}{5}i$ | B. | $\frac{1}{5}+\frac{2}{5}i$ | C. | $-\frac{1}{5}-\frac{2}{5}i$ | D. | $\frac{1}{5}-\frac{2}{5}i$ |
| A. | a≥-2 | B. | a≥2或a≤-2 | C. | -2≤a≤2 | D. | a≤2 |

| A. | 9π | B. | $\frac{9}{2}$π | C. | 6π | D. | 12π |