题目内容
11.化简下列各式(a>0,b>0).(1)(a${\;}^{\frac{2}{3}}$b${\;}^{\frac{1}{2}}$)(-3a${\;}^{\frac{1}{2}}$•b${\;}^{\frac{1}{3}}$)÷($\frac{1}{3}$a${\;}^{\frac{1}{6}}$b${\;}^{\frac{5}{6}}$);
(2)$\frac{\root{3}{{a}^{4}}-8\root{3}{a}•b}{\root{3}{{a}^{2}}+2\root{3}{ab}+4\root{3}{{b}^{2}}}$÷(1-2$\root{3}{\frac{b}{a}}$)×$\root{3}{a}$.
分析 根据指数幂的运算性质计算即可.
解答 解:(1)(a${\;}^{\frac{2}{3}}$b${\;}^{\frac{1}{2}}$)(-3a${\;}^{\frac{1}{2}}$+b${\;}^{\frac{1}{3}}$)÷($\frac{1}{3}$a${\;}^{\frac{1}{6}}$b${\;}^{\frac{5}{6}}$)=-3×3${a}^{\frac{2}{3}+\frac{1}{2}-\frac{1}{6}}$${b}^{\frac{1}{2}+\frac{1}{3}-\frac{5}{6}}$=-9a,
(2)$\frac{\root{3}{{a}^{4}}-8\root{3}{a}•b}{\root{3}{{a}^{2}}+2\root{3}{ab}+4\root{3}{{b}^{2}}}$÷(1-2$\root{3}{\frac{b}{a}}$)×$\root{3}{a}$=$\root{3}{{a}^{\;}}$($\root{3}{a}$-2$\root{3}{b}$)÷(1-2$\root{3}{\frac{b}{a}}$)×$\root{3}{a}$=a(1-2$\root{3}{\frac{b}{a}}$)÷(1-2$\root{3}{\frac{b}{a}}$)=a
点评 本题考查指数幂的运算法则,培养了学生的计算能力,属于基础题.

练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
2.已知F1,F2分别为双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的左、右焦点,若点P是以F1F2为直径的圆与C右支的-个交点,F1P交C于另一点Q,且|PQ|=2|QF1|.则C的渐近线方程为( )
| A. | y=±2x | B. | y=±$\frac{1}{2}$x | C. | y=±$\sqrt{2}$x | D. | y=±$\frac{\sqrt{2}}{2}$x |
19.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的焦距为2c,若$\frac{ab}{{c}^{2}}$取得最大值时,双曲线的离心率等于( )
| A. | $\sqrt{5}$ | B. | 2 | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
6.函数f(x)=(1+$\sqrt{3}$tan2x)cos2x的最小正周期为( )
| A. | 2π | B. | $\frac{3π}{2}$ | C. | π | D. | $\frac{π}{2}$ |
 ,
, ;
; 的解集;
的解集; ,
, ,求
,求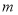 的取值范围.
的取值范围. 为数列的前
为数列的前 项和,已知
项和,已知 ,
, .
. 的通项公式;
的通项公式; ,求数列
,求数列 的前
的前 项和
项和 .
. 是函数
是函数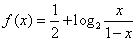 的图象上任意两点,且
的图象上任意两点,且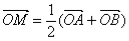 ,点
,点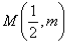 .
.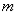 的值;
的值; 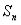 =
=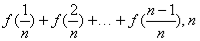 ∈N*,且n≥2,求
∈N*,且n≥2,求 .
. =
= 其中
其中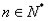 .
. 为数列{an}的前
为数列{an}的前 项和,若
项和,若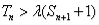 对一切
对一切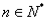 都成立,试求
都成立,试求 的取值范围.
的取值范围. ,则下列各式成立的是( )
,则下列各式成立的是( ) B.
B. C.
C. D.
D.