题目内容
14．计算${∫}_{-2014}^{2014}$（sin7x+$\frac{1}{2}$）dx的值为2014．分析 根据定积分的几何意义和定积分的计算即可．
解答 解：因为积分上下限关于原点对称，且被积函数y=sin7x，故${∫}_{-2014}^{2014}$sin7xdx=0，
${∫}_{-2014}^{2014}$$\frac{1}{2}$dx=$\frac{1}{2}$x|${\;}_{-2014}^{2014}$=2014，
故${∫}_{-2014}^{2014}$（sin7x+$\frac{1}{2}$）dx=0+2014=2014，
故答案为：2014．
点评 本题考查了定积分的几何意义和定积分的计算，属于基础题．
练习册系列答案
阶梯计算系列答案
相关题目
某单位在对一个长800m、宽600m的草坪进行绿化时，是这样想的：中间为矩形绿草坪，四周是等宽的花坛，如图所示，若要保证绿草坪的面积不小于总面积的二分之一．试确定花坛宽度的取值范围．
2．已知F1，F2分别为双曲线C：$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1（a＞0，b＞0）的左、右焦点，若点P是以F1F2为直径的圆与C右支的-个交点，F1P交C于另一点Q，且|PQ|=2|QF1|．则C的渐近线方程为（ ）
| A． | y=±2x | B． | y=±$\frac{1}{2}$x | C． | y=±$\sqrt{2}$x | D． | y=±$\frac{\sqrt{2}}{2}$x |
19．已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1（a＞0，b＞0）的焦距为2c，若$\frac{ab}{{c}^{2}}$取得最大值时，双曲线的离心率等于（ ）
| A． | $\sqrt{5}$ | B． | 2 | C． | $\sqrt{3}$ | D． | $\sqrt{2}$ |
6．函数f（x）=（1+$\sqrt{3}$tan2x）cos2x的最小正周期为（ ）
| A． | 2π | B． | $\frac{3π}{2}$ | C． | π | D． | $\frac{π}{2}$ |
为数列的前
项和，已知
，
.
的通项公式；
，求数列
的前
项和
.
的底面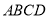
是边长为2的菱形，
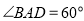，已知
.
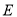为
的中点，求三棱锥
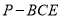的体积.