题目内容
设函数f(x)=ax3-3x2 (a∈R),且x=2是y= f(x)的极值点.
(1)求实数a的值,并求函数的单调区间;
(2)求函数g(x)=ex·f(x)的单调区间.
解 (1)f(x)=3ax2-6x=3x(ax-2),因为x=2是函数y=f(x)的极值点,所以f′(2)=0,即6(2a-2)=0,
因此a=1.
经验证,当a=1时,x=2是 函数y=f(x)的极值点.
函数y=f(x)的极值点.
所以f′(x)=3x2-6x=3x(x-2).
所以y=f(x)的单调增区间是(-∞,0),(2,+∞);
单调减区间是(0,2).
(2)g(x)=ex(x3-3x2),g′(x)=ex(x3-3x2+3x2-6x)=ex(x3-6x)=x(x+ )(x-
)(x- )ex,
)ex,
因为ex>0,所以y=g(x)的单调增区间是(- ,0),(
,0),( ,+∞);单调减区间是(-∞,-
,+∞);单调减区间是(-∞,- ),(0,
),(0, ).
).

练习册系列答案
相关题目
 ,b=(4,4cos α-
,b=(4,4cos α- ),若a⊥b,则sin
),若a⊥b,则sin =________.
=________. 的值是________.
的值是________. 的符号.
的符号. 时,s(t)<3d2成立,则d的取值范围为__________.
时,s(t)<3d2成立,则d的取值范围为__________.
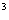 -3ax
-3ax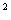 +3bx的图象与直线12x+y-1=0相切于点(1,-
+3bx的图象与直线12x+y-1=0相切于点(1,- 11).
11).
 时,求(∁UB)∩A;
时,求(∁UB)∩A;