题目内容
函数f(x)＝x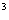
－3ax
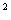＋3bx的图象与直线12x＋y－1＝0相切于点(1，－
11).
(1)求a、b的值；
(2)方程f(x)＝c有三个不同的实数解，求c的取值范围.
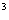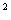解 (1)f(x)＝x－3ax＋3bx，
f′(x)＝3x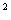－6ax＋3b，f′(1)＝3－6a＋3b＝－12，
f(1)＝1－3a＋3b＝－11，
∴a＝1，b＝－3.
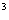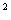(2)f(x)＝x－3x-9x，
f′(x)＝3x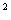－6x－9＝3(x＋1)(x－3)，
当x∈(－∞，－1)，f′(x)>0；
x∈(－1，3)，f′(x)<0；
x∈(3，＋∞)，f′(x)>0.
∴f(x)在x＝－1时取极大值5，在x＝3时取极小值－27.
根据三次函数f(x)的图象得f(x)＝c有三个不同的实数解时，c的取值范围是(－27，5).
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
)在
上单调递增，则ω的最大值为________．
.
是________．