题目内容
设函数f(x)=
x2+ax-lnx(a∈R).
(Ⅰ)若曲线y=f(x)过点P(1,1),求曲线y=f(x)在点P处的切线方程;
(Ⅱ)求函数f(x)在区间[1,2]上的最大值.
| 1-a |
| 2 |
(Ⅰ)若曲线y=f(x)过点P(1,1),求曲线y=f(x)在点P处的切线方程;
(Ⅱ)求函数f(x)在区间[1,2]上的最大值.
考点:利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:函数的性质及应用,导数的综合应用
分析:(1)首先通过导数的几何意义求切线的斜率,然后利用点斜式求方程;
(2)求出函数的导数,讨论f'(x)=0的两根为1,
两根的大小,以及与2的大小比较.
(2)求出函数的导数,讨论f'(x)=0的两根为1,
| 1 |
| a-1 |
解答:
解:(Ⅰ)曲线y=f(x)过点P(1,1),则a=1,f(x)=x-lnx, f′(x)=1-
=
.∵f'(1)=0,∴曲线y=f(x)在点P处的切线方程为y=1.---------------(4分)
(Ⅱ)f(x)的定义域为(0,+∞)f′(x)=(1-a)x+a-
=
=
-------------(5分)
当a=1时,f(x)=x-lnx,f′(x)=1-
=
,得x>1,
∴x∈[1,2]时f'(x)≥0,f(x)单调递增,f(x)max=f(2)=2-ln2;
当1-a>0即a<1时,f'(x)=0的两根为1,
,且1>
,∴x∈[1,2]时f'(x)≥0,f(x)单调递增,f(x)max=f(2)=2-ln2;
当1-a<0即a>1时,f'(x)=0的两根为1,
,
①当 1≥
即a≥2时,x∈[1,2]时f'(x)≤0,f(x)单调递减,f(x)max=f(1)=
;
②当1<
即1<a<2时,x∈(1,
)时f'(x)>0,f(x)单调递增,x∈(
,+∞)时f'(x)<0,f(x)单调递减.
若
≥2即1<a≤
时,x∈[1,2]时f(x)单调递增,f(x)max=f(2)=2-ln2;
若
<2,即
<a<2时,f(x)max=f(
)=
+ln(a-1);
综上,f(x)max=
.---------------------------(12分)
| 1 |
| x |
| x-1 |
| x |
(Ⅱ)f(x)的定义域为(0,+∞)f′(x)=(1-a)x+a-
| 1 |
| x |
| (1-a)x2+ax-1 |
| x |
| [(1-a)x+1](x-1) |
| x |
当a=1时,f(x)=x-lnx,f′(x)=1-
| 1 |
| x |
| x-1 |
| x |
∴x∈[1,2]时f'(x)≥0,f(x)单调递增,f(x)max=f(2)=2-ln2;
当1-a>0即a<1时,f'(x)=0的两根为1,
| 1 |
| a-1 |
| 1 |
| a-1 |
当1-a<0即a>1时,f'(x)=0的两根为1,
| 1 |
| a-1 |
①当 1≥
| 1 |
| a-1 |
| a+1 |
| 2 |
②当1<
| 1 |
| a-1 |
| 1 |
| a-1 |
| 1 |
| a-1 |
若
| 1 |
| a-1 |
| 3 |
| 2 |
若
| 1 |
| a-1 |
| 3 |
| 2 |
| 1 |
| a-1 |
| 2a-1 |
| 2(a-1) |
综上,f(x)max=
|
点评:本题考查了导数的几何意义的运用以及通过求导判断函数的最值,考查了讨论的思想,属于难题.

练习册系列答案
相关题目
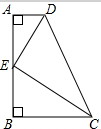 如图,在直角梯形ABCD中,AB⊥AD,AB⊥BC,∠BCD与∠ADC的平分线相交于AB上的一点E,以AB为直径作圆,则该圆与边DC有怎样的位置关系?请说明理由.
如图,在直角梯形ABCD中,AB⊥AD,AB⊥BC,∠BCD与∠ADC的平分线相交于AB上的一点E,以AB为直径作圆,则该圆与边DC有怎样的位置关系?请说明理由.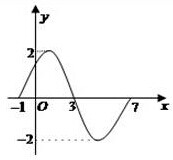 如图为函数y1=Asin(ωx+φ)(|φ|<
如图为函数y1=Asin(ωx+φ)(|φ|<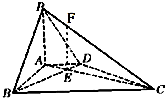 如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AC和BD交于点E,PA=3,AD=2,AB=2
如图,在底面为直角梯形的四棱锥P-ABCD中,AD∥BC,∠ABC=90°,PA⊥平面ABCD,AC和BD交于点E,PA=3,AD=2,AB=2