题目内容
11．已知实数x，y满足$\left\{\begin{array}{l}{y≥x}\\{x+3y≤4}\\{x≥-2}\end{array}\right.$，则z=|3x+y|的最大值是（ ）| A． | 2 | B． | 4 | C． | 6 | D． | 8 |
分析 画出约束条件的可行域，求出三角形的顶点坐标，代入目标函数求解即可．
解答 
解：如图所示，不等式组$\left\{\begin{array}{l}{y≥x}\\{x+3y≤4}\\{x≥-2}\end{array}\right.$所表示的区域为图中阴影部分：
其中A（-2，-2），B（1，1），C（-2，2），zmax=|3×（-2）-2|=8，
故选：D．
点评 本题考查线性规划的应用，交点代入法，是解答线性规划的有效防范之一，考查数形结合以及计算能力．
练习册系列答案
孟建平小学滚动测试系列答案
黄冈天天练口算题卡系列答案
相关题目
2．已知全集U为实数集，集合A={x|x2-2x-3＜0}，B={x|y=ln（1-x）}，则A∩（∁UB）为（ ）
| A． | {x|1≤x＜3} | B． | {x|x＜3} | C． | {x|x≤-1} | D． | {x|-1＜x＜1} |
如图所示，在正方体ABCD-A1B1C1D1中，AB=4，M，N分别为棱A1D1，A1B1的中点，过点B的平面α∥平面AMN，则平面α截该正方体所得截面的面积为18．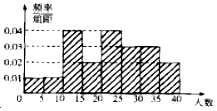
为了更好地让学生适应高考网上阅卷，某学校针对该校20个班级进行了“汉字与英语书法大赛”（每个班级只有一个指导老师），并调查了各班参加该比赛的学生人数，根据所得数据，分组成[0，5），[5，10），[10，15），[15，20），[20，25），[25，30），[30，35），[35，40]时，所作的频率分布直方图如图：