题目内容
8.已知函数f(x)=2cosx(sinx-cosx)+1,x∈R.(1)求函数f(x)的最小正周期;
(2)求函数f(x)在区间$[{0,\frac{π}{2}}]$上的值域.
分析 (1)根据三角恒等变换化简f(x),求出f(x)的最小正周期即可;(2)求出函数的单调区间,从而求出函数的值域.
解答 解:(1)f(x)=2cosx(sinx-cosx)+1
=2cosxsinx-2cosxcosx+1
=sin2x-cos2x
=$\sqrt{2}$sin(2x-$\frac{π}{4}$),
∴函数f(x)的最小正周期T=$\frac{2π}{2}$=π;
(2)f(x)=$\sqrt{2}$sin(2x-$\frac{π}{4}$),
x∈$[{0,\frac{π}{2}}]$,2x-$\frac{π}{4}$∈[-$\frac{π}{4}$,$\frac{3}{4}$π],
由2kπ+$\frac{π}{2}$≤2x-$\frac{π}{4}$≤2kπ+$\frac{3π}{2}$,
解得:kπ+$\frac{3}{8}$π≤x≤kπ+$\frac{7}{8}$π,
∴f(x)在[0,$\frac{3}{8}$π]递增,在[$\frac{3}{8}$π,$\frac{1}{2}$π]递减,
显然x=$\frac{3}{8}$π时,f(x)最大,最大值是$\sqrt{2}$,
x=0时,f(x)最小,最小值是-1,
故f(x)的值域是[-1,$\sqrt{2}$].
点评 本题考查了三角函数的周期及值域,考查三角恒等变换问题,是一道中档题.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
6.下列各函数中,图象经过点($\frac{π}{2}$,-1)的是( )
| A. | y=sinx | B. | y=cosx | C. | y=-sinx | D. | y=-cosx |
20.在等差数列{an}中,a3+a5=12-a7,则a1+a9=( )
| A. | 8 | B. | 12 | C. | 16 | D. | 20 |
17.在一次数学考试中,数学课代表将他们班50名同学的考试成绩按如下方式进行统计得到如下频数分布表(满分为100分)
(Ⅰ)在答题卡上作出这些数据中的频率分布直方图;
(Ⅱ)估计该班学生数学成绩的中位数和平均值;
(Ⅲ)若按照学生成绩在区间[0,60),[60,80),[80,100)内,分别认定为不及格,及格,优良三个等次,用分层抽样的方法从中抽取一个容量为5的样本,计算:从该样本中任意抽取2名学生,至少有一名学生成绩属于及格等次的概率.
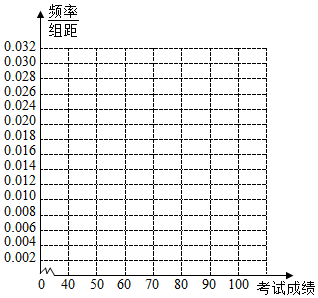
| 成绩 | [40,50) | [50,60) | [60,70) | [70,80) | [80,90) | [90,100) |
| 人数 | 2 | 8 | 15 | 15 | 4 | 6 |
(Ⅱ)估计该班学生数学成绩的中位数和平均值;
(Ⅲ)若按照学生成绩在区间[0,60),[60,80),[80,100)内,分别认定为不及格,及格,优良三个等次,用分层抽样的方法从中抽取一个容量为5的样本,计算:从该样本中任意抽取2名学生,至少有一名学生成绩属于及格等次的概率.

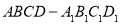 内接于半径为
内接于半径为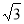 的半球
的半球 ,四边形
,四边形 为正方形,则该四棱柱的体积最大时,
为正方形,则该四棱柱的体积最大时,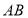 的长为( )
的长为( )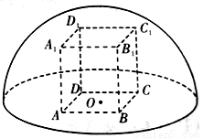
 B.
B.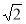 C.
C.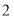
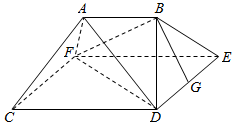 如图,在多面体ABCDEF中,四边形CDEF是正方形,AB∥CD,CD=2AB,G为DE的中点.
如图,在多面体ABCDEF中,四边形CDEF是正方形,AB∥CD,CD=2AB,G为DE的中点.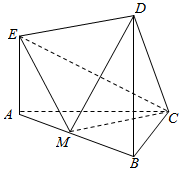 在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.
在如图所示的几何体中.EA⊥平面ABC,DB⊥平面ABC,AC⊥BC,且AC=BC=BD=2AE=2,M是AB的中点.