题目内容
16.若直线1的倾斜角是120°,且该直线过点(1,k)和(-2,0),则k=( )| A. | -3$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | -$\sqrt{3}$ | D. | $\sqrt{3}$ |
分析 求出直线的斜率,设出直线的方程,代入点的坐标,求出直线方程即可.
解答 解:∵倾斜角是120°,斜率是:-$\sqrt{3}$,
设直线l的方程是y=-$\sqrt{3}$x+b,
故-$\sqrt{3}$+b=k,-2$\sqrt{3}$+b=0,
解得:k=$\sqrt{3}$,
故选:D.
点评 本题考查了直线的斜率问题,考查求直线方程问题,是一道基础题.

练习册系列答案
相关题目
6.设集合A={x|x2-2x≥0},B={x|-1<x<2},则A∩B=( )
| A. | {x|0≤x≤2} | B. | {x|0<x<2} | C. | {x|-1≤x<0} | D. | {x|-1<x≤0} |
7.函数f(x)为奇函数,则函数$\frac{{3}^{x}-1}{{3}^{x}+1}$•f(x)为( )
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 既是偶函数,也是奇函数 | D. | 既非偶函数,也非奇函数 |
5.已知x是x1,x2,…,x10的平均值,a1为x1,x2,x3,x4的平均值,a2为x5,x6,x10的平均值,则x=( )
| A. | $\frac{2{a}_{1}+3{a}_{2}}{5}$ | B. | $\frac{3{a}_{1}+2{a}_{2}}{5}$ | C. | a1+a2 | D. | $\frac{{a}_{1}+{a}_{2}}{2}$ |
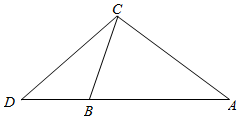 如图,在锐角三角形ABC中,∠A=$\frac{π}{4}$,AC=$\sqrt{3}$,BC=$\sqrt{2}$,BD=$\frac{3\sqrt{2}}{5}$;
如图,在锐角三角形ABC中,∠A=$\frac{π}{4}$,AC=$\sqrt{3}$,BC=$\sqrt{2}$,BD=$\frac{3\sqrt{2}}{5}$;